Основные уравнения электродинамики в дифференциальной форме, страница 2

Пусть имеется однородная проводящая среда σ≠ 0, в которой отсутствуют сторонние источники =0, =0, тогда третье уравнение системы (2.7) запишется так:

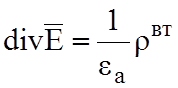
Из уравнения (2.8)

,

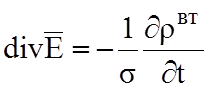приравнивая их, получим уравнение:

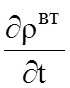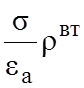+=0,

его решение

,

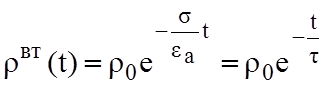где 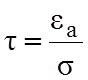 – время релаксации, то есть время, в течении которого первоначальный вторичный заряд  убывает в ℮=2,71 раз. Для  морской воды τ=10^–6 с, для меди τ=10^–8, то есть заряд быстро убывает и можно считать, что в проводящей среде 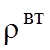=0, существование ЭМП не сопровождается возникновением свободных зарядов.

При σ=0 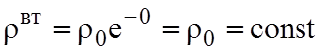, заряды могут длительно сохраняться, нет релаксации, нет движения зарядов, нет токов. Это же следует из закона сохранения зарядов:

;

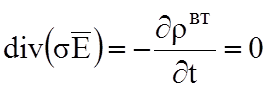так как σ=0, отсюда 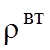=const.

Граничные условия в ЭМП. Поверхность, разделяющая среды, отличающиеся по макроскопическим параметрам ε_а, μ_а, σ есть граничная поверхность или поверхность раздела двух сред, которая может быть плоской, сферической или любой другой. При прохождении ЭМВ через границу раздела изменяются ее параметры, все, кроме частоты.  Изменяются амплитуда, фаза, скорости распространения, направление. Поведение векторов при переходе границы описывают граничные уравнения, или условия. Если ЭМП существует, то граничные условия выполняются, если граничные условия выполняются, то в этих условиях ЭМП может существовать. Если граничные условия не выполняются, то ЭМП существовать не может. Поэтому, чтобы решение электродинамической задачи можно было физически реализовать на практике, в решение задачи закладывают граничные условия. Выполнение граничных условий требуют при анализе электромагнитных явлений при различных теоретических выводах, при решении практических задач. Это фундаментальные законы природы, которые всегда выполняются. Получают граничные условия из интегральных уравнений Гаусса, Фарадея, закона полного тока путем предельного перехода, а именно, путем сжатия высоты цилиндра или контура к нулю. Так получают условия на границе. Уравнения в дифференциальной форме на границе не справедливы, так как ε_а, μ_а, σ изменяются скачком.

Векторы , , ,  направлены к границе под любым углом. Каждый вектор представляют как сумму двух векторов – нормальный и касательный к границе, и граничные условия получают отдельно для нормальных и касательных составляющих векторов поля (рисунок 2.1).

Рисунок 2.1

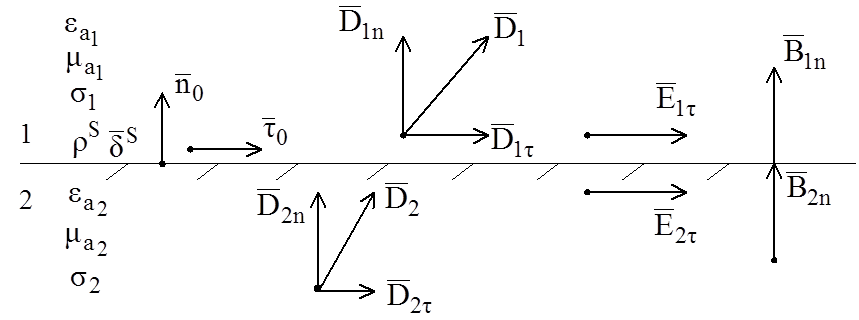Рисунок 2.2

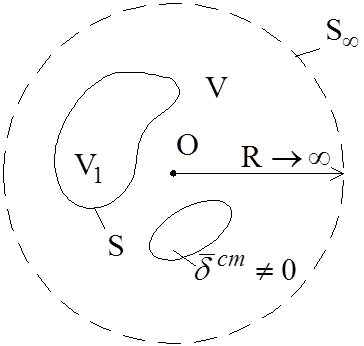Рисунок 2.3

Граница раздела может иметь поверхностный заряд , или по ней протекают поверхностные токи .

Граничные условия для нормальных составляющих векторов поля:

1. 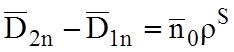 , если 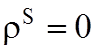, то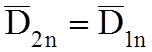

2. 

Нормальная составляющая вектора при переходе границы не терпит разрыва.

Используя связь векторов и , и, получают граничные условия для нормальных составляющих  и .

Граничные условия для касательных составляющих векторов поля:

3. 

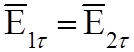
4. 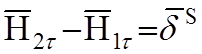 , если ,то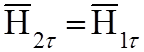

Касательные, составляющие к границе векторов  и , всегда равны,

т.е. не терпят разрыва.

Уравнение Максвелла в комплексной форме. Метод комплексных

амплитуд. В систему уравнений Максвелла входят частные производные по четырем независимым переменным – x, y, z, t. Для упрощения решения можно исключить зависимость от времени, если рассматриваемый электромагнитный процесс является монохроматическим, т.е. изменение полей во времени представляется гармоническими колебаниями одной частоты w, любой закон изменения во времени можно получить, воспользовавшись методом интеграла Фурье. Вектор , изменяющийся по гармоническому закону в некоторой точке пространства записывается в виде:

,

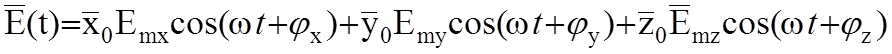где , , 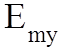, , ,  - амплитуды отдельных составляющих вектора и их фазовые углы, это вещественные числа. Согласно формуле Эйлера (для одной составляющей для упрощения записи) можно записать так:

.

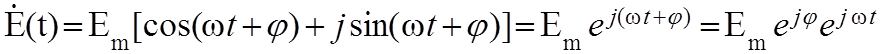Реальный физический процесс протекает по закону вещественной части комплексного числа .

Временной множитель при такой записи в уравнениях сокращается,

остается 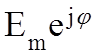 , который называют комплексной амплитудой 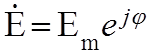. С учетом комплексной амплитуды можно записать:

,  

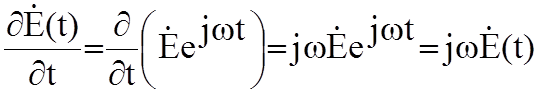
Дифференцирование комплексной величины равносильно умножению ее на оператор jw, а интегрирование – делению на jw. Запишем уравнения Максвелла для комплексных амплитуд.

          ,

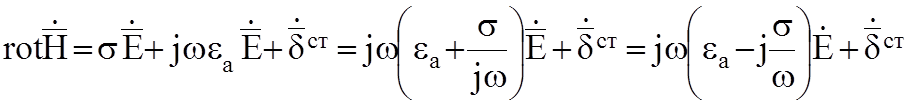где 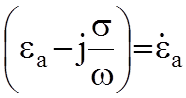 комплексная диэлектрическая проницаемость среды,

с учетом этого:

1. 

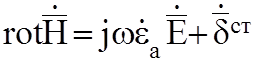
2. 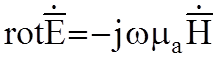                                                                                      (2.9)

Это можно считать полная система уравнений Максвелла, третье и четвертое уравнения вытекают из первого и второго, как следствие.

Угол диэлектрических потерь. В реальных средах всегда s¹0, значит

имеются токи проводимости, и если ЭМП переменное, то и токи смещения. Если в среде преобладают токи проводимости, то среда близка к проводникам, а если токи смещения, то к диэлектрикам, то есть нужно оценивать отношение этих токов, точнее плотностей этих токов.

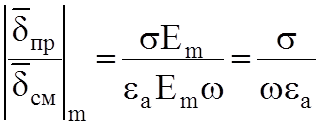                                               (2.10)

Введение комплексной диэлектрической проницаемости позволяет учитывать как диэлектрические, так и проводящие свойства данного вещества. Вещественная часть говорит об интенсивности процесса поляризации, мнимая часть характеризует плотность токов проводимости.

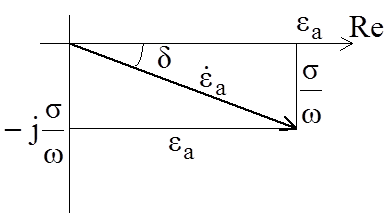
Изображая на комплексной плоскости можно характеризовать соотношение между вещественной и мнимой частями при помощи угла d, носящего название угла диэлектрических потерь. Чем больше этот угол, тем относительно большая часть электромагнитной энергии рассеивается в виде тепла при протекании токов проводимости (рисунок 2.2). На практике, пользуясь тангенсом этого угла, с учетом формулы (2.10) запишется:

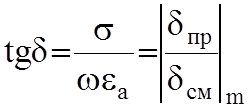                                                         (2.11)

Для хороших диэлектриков tgd=10^-4… 10^-3, он характеризует свойства сред как функцию от частоты. Одна и та же среда на низких и высоких частотах резко отличается по свойствам. Например, сухая почва на частоте 5×10³ Гц имеет tgd@10² , то есть проводник, а на СВЧ f=10⁸ Гц становится диэлектриком tgd@10^-3 .