



Магнитных
зарядов в природе не существует, это утверждается уравнением ![]() . Для облегчения расчетов их вводят в
рассмотрение в качестве фиктивных, воображаемых QМ , тогда они будут создавать фиктивный магнитный ток с
плотностью
. Для облегчения расчетов их вводят в
рассмотрение в качестве фиктивных, воображаемых QМ , тогда они будут создавать фиктивный магнитный ток с
плотностью ![]() , который может быть источником ЭМП. В этом
случае, второе уравнение Максвелла надо записать так:
, который может быть источником ЭМП. В этом
случае, второе уравнение Максвелла надо записать так:
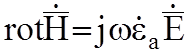 ;
; 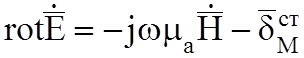 (7.1)
(7.1)
Принцип перестановочной двойственности заключается в том, что перестановка:
![]() ,
, ![]() ,
, 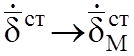 ,
,
![]() ,
, ![]() ,
, 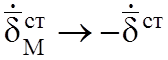 (7.2)
(7.2)
преобразует
систему уравнений (2.9) в систему (7.1) и наоборот. Отсюда следует важный
вывод. Если известно решение системы (2.9) для электрических источников ![]() , то, используя замену, можно без решения
задачи для
, то, используя замену, можно без решения
задачи для ![]() получить решение для магнитных источников
получить решение для магнитных источников ![]() .
.
7.1 Элементарный магнитный излучатель
Если
в элементарном электрическом излучателе ![]() заменить
на
заменить
на ![]() , то получим элементарный магнитный
излучатель (ЭМИ). Электромагнитное поле в дальней зоне для ЭМИ получается путем
замены по (7.2), где
, то получим элементарный магнитный
излучатель (ЭМИ). Электромагнитное поле в дальней зоне для ЭМИ получается путем
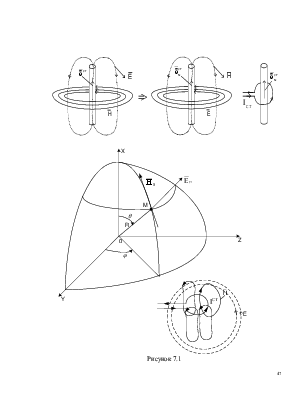
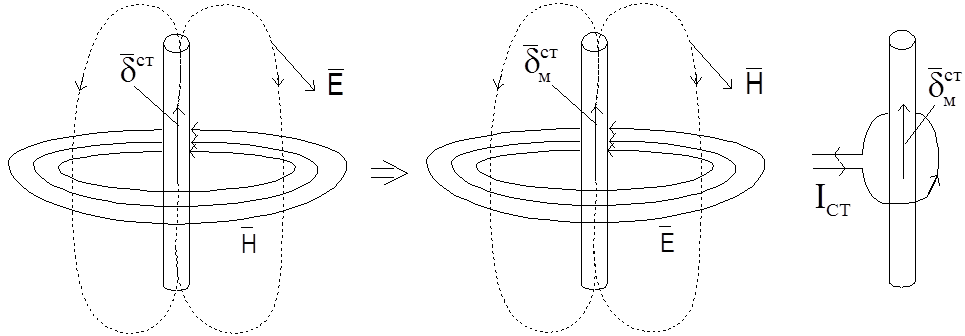
замены по (7.2), где 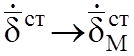 равносильно замене
равносильно замене ![]() (рисунок 7.1):
(рисунок 7.1):
 ;
;
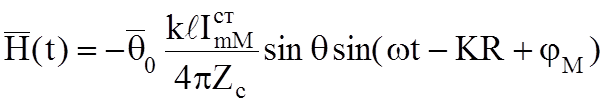 (7.3)
(7.3)
как
видно из (7.3) векторы ![]() и
и ![]() поменялись
местами. Физической моделью ЭМИ является плоская проводящая рамка с током
поменялись
местами. Физической моделью ЭМИ является плоская проводящая рамка с током ![]() , периметр которого весьма мал по сравнению
с длиной волны l, то есть
, периметр которого весьма мал по сравнению
с длиной волны l, то есть ![]() , где S-
площадь кругового тока
, где S-
площадь кругового тока ![]() . Тогда в (7.3)
. Тогда в (7.3) ![]() . Такой излучатель называют элементарной
электрической рамкой, максимум излучения ее лежит в плоскости
. Такой излучатель называют элементарной
электрической рамкой, максимум излучения ее лежит в плоскости
рамки,
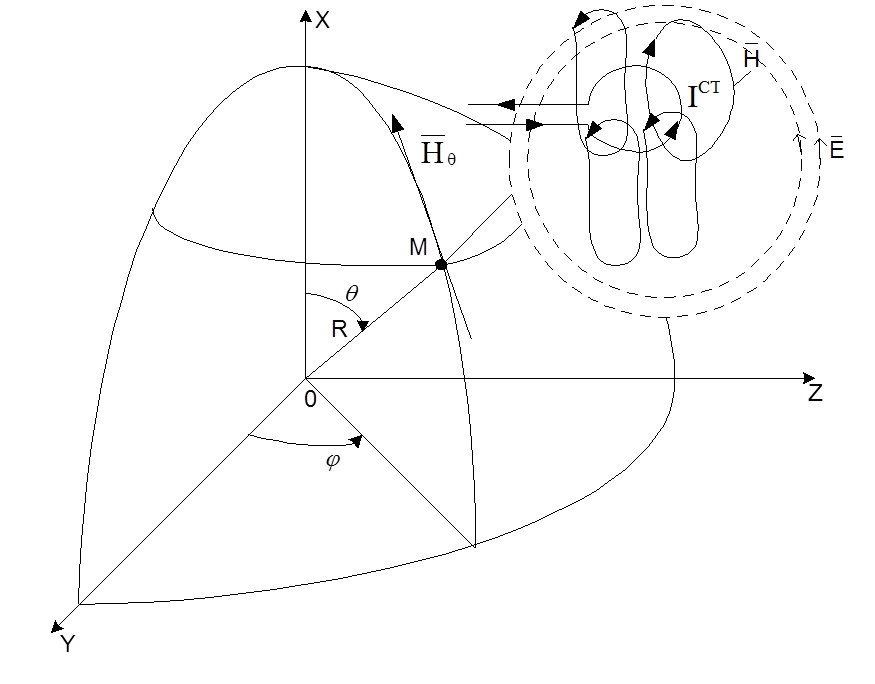
по нормали к плоскости рамки излучения нет. Для рамки вводится эквивалентная
длина ![]() , тогда ЭМП рамки в дальней зоне имеет вид:
, тогда ЭМП рамки в дальней зоне имеет вид:
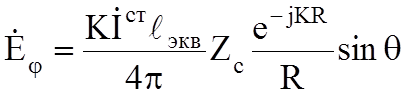
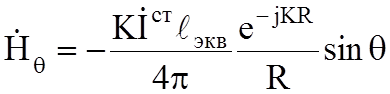 (7.4)
(7.4)
Мощность излучения рамки:
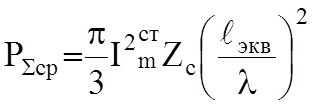
Сопротивление излучения рамки:
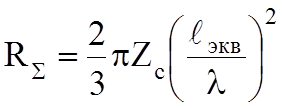
Отношение сопротивлений излучения ЭЭИ и ЭМИ равно:
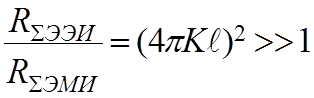
излучающая способность ЭЭИ (открытая система) значительно больше ЭМИ (закрытая система). Поэтому электрические излучатели в основном используют в качестве передающих антенн, а магнитные (рамка) – в качестве приемных.
7.2 Принцип взаимности
Простой
вариант принципа взаимности можно получить следующим образом. Пусть источники
ЭМП ![]() находятся в объеме V1
и создают электрическое поле в
объеме V2 равное
находятся в объеме V1
и создают электрическое поле в
объеме V2 равное ![]() , аналогично, источники, находящиеся в
объеме V2 создают
электрическое поле
, аналогично, источники, находящиеся в
объеме V2 создают
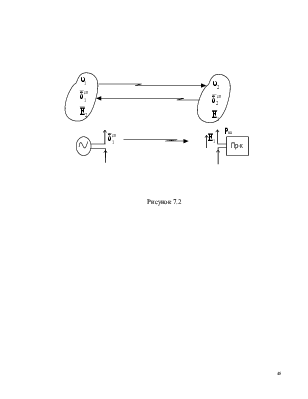
электрическое поле ![]() в объеме V1. (Рисунок 7.2). Тогда принцип взаимности запишется
следующим образом:
в объеме V1. (Рисунок 7.2). Тогда принцип взаимности запишется
следующим образом:
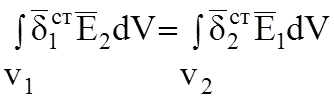 (7.5)
(7.5)
Если
распределения токов ![]() в объеме V1 одинаково с таковым
в объеме V1 одинаково с таковым ![]() в
объеме V2, то и
одинаковы создаваемые ими электрические поля
в
объеме V2, то и
одинаковы создаваемые ими электрические поля ![]() . Или,
еще проще. Пусть в V1
находится передающая антенна с
. Или,
еще проще. Пусть в V1
находится передающая антенна с ![]() , а в объеме V2 – приемная, мощность на входе приемника РВХ.
Теперь поменяем местами антенны, передающую антенну поместим и расположим ее
так же как была расположена приемная антенна, а приемную антенну поместим на
месте передающей. Тогда в линейной изотропной среде, согласно принципа,
взаимности мощность на входе
, а в объеме V2 – приемная, мощность на входе приемника РВХ.
Теперь поменяем местами антенны, передающую антенну поместим и расположим ее
так же как была расположена приемная антенна, а приемную антенну поместим на
месте передающей. Тогда в линейной изотропной среде, согласно принципа,
взаимности мощность на входе
 |
 |
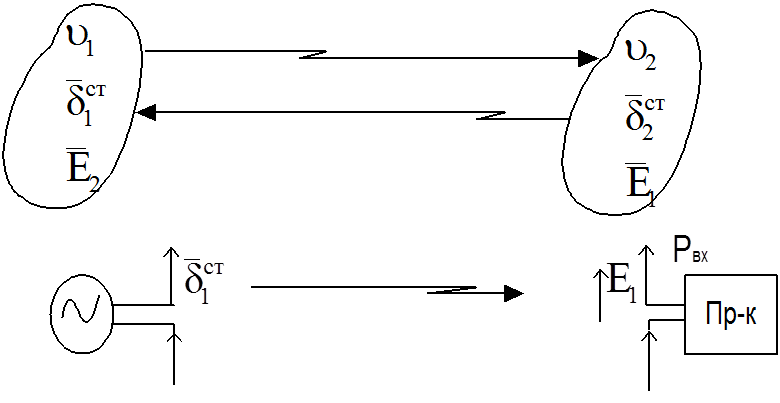 |
приемника будет такой же, то есть не изменится. Во втором случае изменилось направление распространения ЭМВ на обратное, а РВХ осталась неизменной. Это говорит о том, что напряженность электрического поля в изотропной среде не зависит от направления распространения ЭМВ. В антенной технике на основании принципа взаимности развивается теория приемных антенн, а именно любая антенна имеет одинаковые электрические параметры (ДН, Zвх, RS и др.) как в режиме передачи, так и в режиме приема. Поэтому антенну исследуют в одном режиме, в режиме передачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.