7.3 Принцип эквивалентности
Пусть
реальные источники  расположены в объеме V1, ограниченном поверхностью S, они могут
быть неизвестными или заданы сложной зависимостью, но предполагаются известными
значения касательных составляющих создаваемого ими поля
расположены в объеме V1, ограниченном поверхностью S, они могут
быть неизвестными или заданы сложной зависимостью, но предполагаются известными
значения касательных составляющих создаваемого ими поля ![]() и
и
![]() на поверхности S. Этого
достаточно, согласно теореме единственности, для нахождения ЭМП вне объема V1. Касательные составляющие
на поверхности S. Этого
достаточно, согласно теореме единственности, для нахождения ЭМП вне объема V1. Касательные составляющие ![]() и
и ![]() можно выразить через эквивалентные им
поверхностные токи
можно выразить через эквивалентные им
поверхностные токи ![]() и
и ![]() электрические
и магнитные. Эти поверхностные токи называют эквивалентными источниками, их
можно рассчитать или измерить на любой поверхности S, окружающей
истинные источники
электрические
и магнитные. Эти поверхностные токи называют эквивалентными источниками, их
можно рассчитать или измерить на любой поверхности S, окружающей
истинные источники  . Плотность эквивалентного
электрического тока определяется касательной составляющей вектора
. Плотность эквивалентного
электрического тока определяется касательной составляющей вектора ![]() , а плотность эквивалентного магнитного
тока – касательной вектора
, а плотность эквивалентного магнитного
тока – касательной вектора ![]() :
:
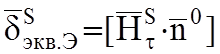 ;
; 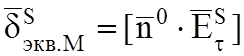 (7.6)
(7.6)
Для расчета эквивалентных источников применяют приближенные методы, основанные на идеях Гюйгенса и Кирхгофа.
7.4 Принцип Гюйгенса – Френеля. Элемент Гюйгенса
Сторонние
источники 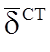 , распределенные в объеме, в каждой точке
создают в точке наблюдения элементарную сферическую волну с векторами
, распределенные в объеме, в каждой точке
создают в точке наблюдения элементарную сферическую волну с векторами ![]() и
и ![]() . Полное
поле в точке наблюдения является результатом суперпозиции всех элементарных
сферических волн, которые создаются в этой точке сторонними источниками,
распределенными с плотностями
. Полное
поле в точке наблюдения является результатом суперпозиции всех элементарных
сферических волн, которые создаются в этой точке сторонними источниками,
распределенными с плотностями 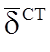 в объеме V, то
есть:
в объеме V, то
есть:
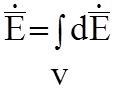 ,
, 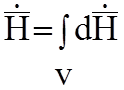
То
же самое можно сказать относительно вторичных, эквивалентных источников,
находящихся на поверхности S, окружающей истинные источники 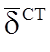 .
.
Отсюда формулируется принцип Гюйгенса – Френеля, согласно которому каждый элемент произвольной замкнутой поверхности, окружающей источники поля, можно рассматривать как вторичный источник новой элементарной сферической волны, а поле в точке наблюдения – как суперпозицию этих элементарных вторичных волн.
При
решении задач удобно совмещать поверхность S с волновой
поверхностью поля, тогда касательные составляющие векторов ![]() и
и ![]() ,
которые определяют вторичные источники на волновой поверхности, можно считать
связанными между собой
,
которые определяют вторичные источники на волновой поверхности, можно считать
связанными между собой ![]() и взаимно
перпендикулярными.
и взаимно
перпендикулярными.
Элементом
Гюйгенса называют элемент dS волновой поверхности бегущей волны, линейные размеры
которого много меньше длины волны l, поэтому его можно
считать плоским и в пределах которого ![]() и
и ![]() являются постоянными. Касательные
составляющие
являются постоянными. Касательные
составляющие ![]() и
и ![]() определяют
эквивалентные источники, электрические и магнитные (7.6), которые в свою
очередь можно представить как электрические и магнитные токи, то есть
элементарные электрический излучатель (ЭЭИ) и магнитный (ЭМИ). Электромагнитные
поля в дальней зоне для ЭЭИ и ЭМИ известны.
определяют
эквивалентные источники, электрические и магнитные (7.6), которые в свою
очередь можно представить как электрические и магнитные токи, то есть
элементарные электрический излучатель (ЭЭИ) и магнитный (ЭМИ). Электромагнитные
поля в дальней зоне для ЭЭИ и ЭМИ известны.
Таким
образом, элемент Гюйгенса можно представить как совокупность
взаимноперпендикулярных ЭЭИ и ЭМИ, а ЭМП элемента Гюйгенса как сумму их полей с
учетом амплитуд и фаз. В результате ДН элемента Гюйгенса имеет следующий вид: ![]() , где q - угол
отсчитываемый от нормали и плоскости dS элемента.
, где q - угол
отсчитываемый от нормали и плоскости dS элемента.
В
дальней зоне ЭМП элемента Гюйгенса присущи все основные особенности поля
излучения элементарных излучателей. Это поле представляет собой вторичные
элементарные сферические волны, расходящиеся в полупространстве Z>0
от элемента Гюйгенса вдоль радиусов R в бесконечность со скоростью 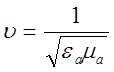 и убывающие по амплитуде по закону 1/R.
Амплитудная характеристика направленности
и убывающие по амплитуде по закону 1/R.
Амплитудная характеристика направленности ![]() не
зависит от азимутального угла j, имеет максимум при q=0, равный двум. Часто используют нормированную
не
зависит от азимутального угла j, имеет максимум при q=0, равный двум. Часто используют нормированную ![]() характеристику,
ее обозначают
характеристику,
ее обозначают 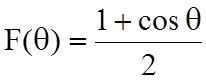 . Графическое изображение ее
представляет собой кардиоиду. При q=p, F(q)=0, то есть нет
излучения элемента dS в строну первичного источника
. Графическое изображение ее
представляет собой кардиоиду. При q=p, F(q)=0, то есть нет
излучения элемента dS в строну первичного источника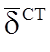 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.