Теплотехнические измерения и инновационные измерительные технологии, страница 6

В жидкостных манометрических термометрах может иметь место гидростатическая погрешность, вызываемая различными уровнями расположения термобаллона и измерительного прибора. Для уменьшения этой погрешности длину капилляра сокращают до 10 м. Предельные уровни размещения термобаллона и измерительного прибора относительно друг друга оговариваются в инструкциях к прибору.

Конденсационные манометрические термометры применяются для измерения температуры в диапазоне от – 50 до + 300 °C. Термобаллон заполняется на ¾ объема низкокипящей жидкостью, а остальная часть – насыщенным паром этой жидкости. Количество жидкости в термобаллоне должно быть таким, чтобы не вся жидкость при максимальной температуре превращалась в пар. В качестве рабочей жидкости используется фреон-22, пропилен, хлористый метил, ацетон и этилбензол. Капилляр и манометрическая пружина заполняются, как правило, другой жидкостью. Давление в термосистеме равно давлению насыщенного пара рабочей жидкости, соответствующего измеряемой температуре среды, в которой помещен термобаллон. Зависимость давления насыщения от температуры нелинейная, но однозначная функция, если измеряемая температура не превышает критической.

Т. к. давление в термосистеме зависит только от измеряемой температуры, то влияние изменения температуры окружающей среды на показания прибора не будет. Гидростатическая погрешность от наличия разности уровней размещения термобаллона и измерительного прибора будет иметь место, причем в начале шкалы она больше, а в конце – меньше. Поэтому длину капилляра ограничивают до 25 м. Барометрическая погрешность проявляется только в начале шкалы, а в остальном диапазоне она пренебрежимо мала.

Специальные конденсационные манометрические термометры используются для измерения сверхнизких температур, например, от 0,8 K.

К достоинствам манометрических термометров относятся: простота устройства, возможность дистанционной передачи и автоматической записи, использование в пожаро- и взрывоопасных помещениях. В качестве недостатков следует указать: трудность ремонта или разгерметизации термосистемы, ограничения дистанционной передачи, большие размеры термобаллона. Газовые и жидкостные манометрические термометры выпускаются с классом точности 1; 1,5; 2,5, а конденсационные – 1,5; 2,5 и 4.

5.2.3.  Термоэлектрические термометры

В основу применения термоэлектрических термометров для измерения температуры положена зависимость термоэлектродвижущей силы (ТЭДС) термопары от температуры. ТЭДС возникает в цепи, составленной из двух (1 и 2, рис. 5.4) разнородных проводников при неравенстве температур в местах соединения этих проводников (а и б).

Современная физика объясняет термоэлектрическое явление как следствие возникновения контактной разности потенциалов из-за различия уровней Ферми у различных металлов и как результат диффузии свободных электронов под действием разности температур, приводящей к образованию электрического поля. Таким образом, ТЭДС слагается из суммы скачков потенциала в спаях термопары и суммы изменений потенциала из-за диффузии свободных электронов, она зависит от рода проводников и их температуры.

Если температуры в спаях одинаковы (t = t₀), то разности потенциалов будут равны по значению, но иметь разные знаки:

                                                          ,                          

а суммарная ТЭДС и ток в цепи равны нулю:

                                                .         (5.6)

В случае, когда , суммарная ТЭДС не равна нулю:

                                                .         (5.7)

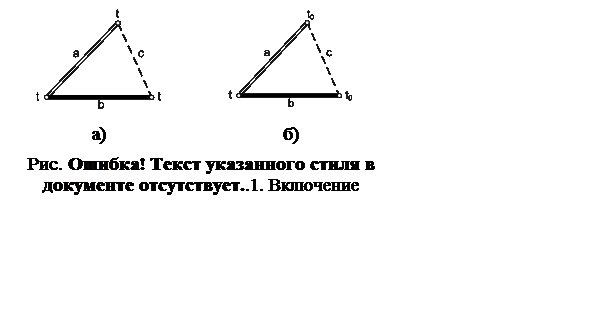При включении в цепь термоэлектрического термометра третьего проводника (рис. 5.5) в случае, когда все спаи проводников a, b, c (пример а) будут иметь одинаковую температуру t, суммарная ТЭДС составит:

                                        , (5.8)

или                                           .

Но когда температуры спаев неодинаковы (пример б), т. е. температура третьего проводника c не равна температуре измеряемой, то