Теплотехнические измерения и инновационные измерительные технологии, страница 32

Предположим, что протекает через сужающее устройство несжимаемая жидкость. Закон сохранения энергии для сечений A и B может быть представлен в виде уравнения Бернулли

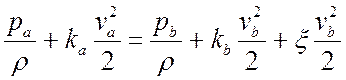                                            ,   (5.46)

где     k_a, k_b – поправочные коэффициенты на неравномерность распределения скоростей в сечениях A и B;

          v_a, v_b – средние скорости потока в сечениях A и B;

          x – коэффициент сопротивления на участке AB, отнесенный к скорости v_b.

Из условия сплошности потока плотностью r, движущегося по трубе сечением F со скоростью v, расход выражается формулой . Тогда, исходя из равенства массовых расходов в сечениях A и B, справедливо соотношение

                                                           ,                  (5.47)

где     F_a, F_b – площади струи в сечениях A и B.

Обозначим площадь отверстия сужающего устройства F₀. Отношение F₀ к площади сечения трубопровода F называется модулем сужающего устройства

                                                        ,

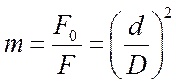где     d, D – диаметры отверстия сужающего устройства и трубы.

Отношение  называется коэффициентом сужения струи.

После преобразования (5.47) получим:

                                                            .

Подставляя это выражение в (5.47), выразим:

                                      .

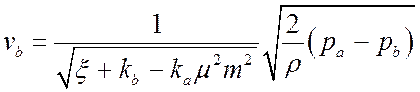Учитывая, что измерение давлений производится сразу до и после сужающего устройства p₁ и p₂, введем коэффициент 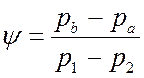, тогда

                                       .

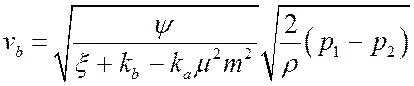Имея в виду, что , окончательно получим выражение для массового расхода:

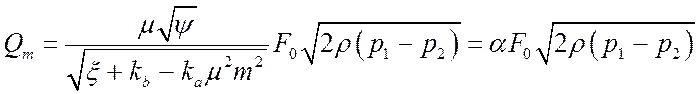      .                                                                (5.48)

С учетом связи 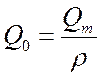 выражение для объемного расхода имеет вид:

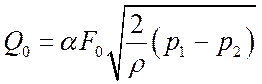                                                  .         (5.49)

Величина a называется коэффициентом расхода.

В случае измерения газа или пара, т. е. для сжимаемых сред, при протекании через сужающее устройство происходит изменение плотности r вследствие изменения давления. Это обстоятельство учитывается введением в уравнения (5.48) и (5.49) поправочного множителя e – коэффициента расширения измеряемой среды. Тогда для сжимаемых сред уравнение расхода принимает вид:

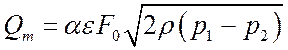                                                ,       (5.50)

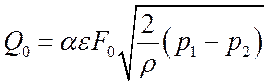                                                 .        (5.51)

Величина e для несжимаемых сред равна единице, а для сжимаемых сред она зависит от соотношения 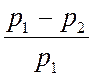. Т. к. с изменением расхода изменяется , то будет изменяться и e. Поэтому в расчетах градуировочной характеристики используют среднее значение e_ср, ориентируясь на номинальный режим работы установки при среднем расходе как на наиболее вероятный режим.

При работе расходомерного устройства предполагается, что F₀, a не должны зависеть от расхода. Однако существующие конструкции сужающих устройств обеспечивают практическое постоянство значений коэффициента расхода a только в определенном ограниченном интервале изменения расхода (точнее, чисел Рейнольдса Re). Поэтому важнейшим условием применения сужающих устройств является требование обеспечения определенной скоростной характеристики потока, т. е. Re > Re_min. Значение Re_min представляет границу применения градуировочной характеристики, на которую рассчитан расходомер.

Серьезным недостатком метода является суженный диапазон измерения каждого конкретного расходомера, охватывающего обычно 30 – 100 % максимального измеряемого расхода Q_в.п. Следовательно, в интервале 0 – 30 % шкалы расходомера использовать нельзя, т. к. здесь не гарантируется достаточная точность измерения.

Недостаток метода и в том, что зависимость перепада давления и расхода квадратичная. Это определяет квадратичный характер шкалы прибора (неравномерный). Для получения равномерной шкалы требуется применение специальных устройств для извлечения квадратного корня, что снижает точность измерения.