Теоретические основы теплотехники. Тепломассообмен: Задания на курсовое проектирование и методические указания к выполнению, страница 5

Тогда отношение действительного теплового потока к максимальному оценивает коэффициент эффективности продольного ребра прямоугольного сечения:

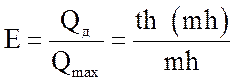                                                    .              (26)

Используя зависимости (21), (24), (26), рассчитать распределение температуры по высоте ребра , потока теплоты и эффективность ребра в условиях свободной конвекции и вынужденного движения воздуха относительно не­оребренной и оребренной плоской стенок.

 В условиях свободной конвекции коэффициент теплообмена  можно опре­делить по критериальным уравнениям [4]:

                             1)  при ;                                                                  (27)

                    2)  при ,                                                                  (28)

где 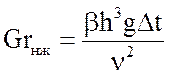     – критерий Грасгофа;

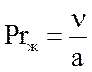           – критерий Прандтля;

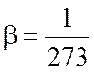           – температурный коэффициент объемного расширения воздуха.

При расчете  в условиях вынужденного движения можно воспользо­ваться выражением:

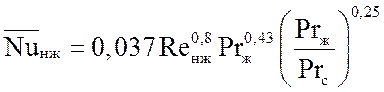                                         .   (29)

За определяющие температуру и размер принять соответственно темпера­туру в основании ребра t₁ и длину ребра H.

3. Теплообмен при пленочной конденсации пара

Если пар соприкасается со стенкой, температура которой ниже температуры насыщения t_s, то он конденсируется, и конденсат оседает на стенке.

Конденсация может быть капельная, когда конденсат оседает на поверхно­сти в виде отдельных капель, пленочная, когда на поверхности образуется сплошная пленка жидкости, и объемная – в виде отдельных капель внутри объема пара или парогазовой смеси за счет перенасыщения пара (его плот­ность больше плотности насыщенного пара).

В промышленных теплообменных аппаратах чаще встречается пленочная конденсация.

Аналитическое решение задачи теплообмена при пленочной конденсации выполнено Нуссельтом для неподвижного сухого насыщенного пара.

Средняя величина коэффициента теплообмена при конденсации сухого на­сыщенного пара на вертикальной стенке высотой h для ламинарного движе­ния конденсатной пленки определяется по формуле:

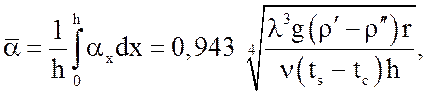                                      (30)

где     l – коэффициент теплопроводности жидкости, ;

          r′ и r″ – соответственно плотность жидкости и сухого насыщенного пара, ;

          r – удельная теплота фазового перехода,

          n – коэффициент кинематической вязкости жидкости, ;

          h – высота вертикальной стенки, м;

          t_c – температура стенки,

          a_x – локальный коэффициент теплообмена, .

Преобразуя (30) с использованием критериев:

Нуссельта 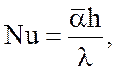                                                                 (31)

Архимеда 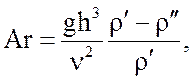                                                      (32)

Прандтля 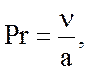                                                                      (33)

Кутателадзе 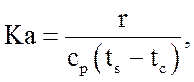                                                  (34)

получаем критериальное уравнение:

                                                          (35)

в котором за определяющую принимается температура фазового перехода, а за определяющий размер – высота вертикальной поверхности h, м.

Критериальное уравнение теплообмена при конденсации пара на горизон­тальной трубе с внешним диаметром d, принятым за определяющий размер вместо высоты h, имеет вид:

                                                          (36)

При выполнении задания необходимо произвести расчеты для выяснения влия­ния давления пара, его степени сухости и степени перегрева, концентрации воздуха в паре, скорости потока пара, температурного напора  а также геометрических определяющих размеров теплообменной поверхности на коэффициент теплоотдачи при вертикальном и горизонтальном расположении одиночной трубки и построить соответствующие зависимости.