Теоретические основы теплотехники. Тепломассообмен: Задания на курсовое проектирование и методические указания к выполнению, страница 4

 Достаточная точность вычислений достигается с использованием лишь не­скольких первых членов ряда, а при малых значениях критерия Bi <<1 (тонкие стенки с большой теплопроводностью) можно получить удовлетво­рительные результаты при одном первом значении корня .

Температура в середине плиты определяется при х = 0:

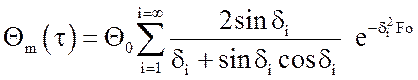                                       . (12)

Температура на поверхности плиты при 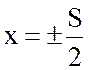 находится по формуле:

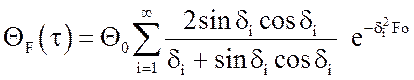                                       . (13)

Количество тепла, подведенное через единицу площади поверхности при ее нагреве от начальной температуры до температуры, равной температуре потока пара, определится по формуле,

                                                                               (14)

а количество тепла, подведенное к единице площади поверхности за время  с обеих сторон плиты, –

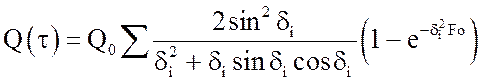                                  .                                                                  (15)

Для проверки результатов расчетов можно воспользоваться графическими зависимостями:

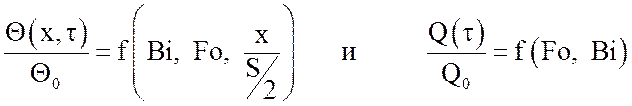                ,                                                                  (16)

приведенными в [1 – 3].

Значение среднего коэффициента теплообмена между потоком пара и пли­той для упрощения расчетов можно определить исходя из условия смешан­ного режима течения взаимодействующего потока с поверхностью, приняв условно критическое значение числа Рейнольдса Re_кр = , по уравнению [2]:

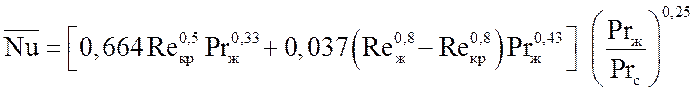       ,                                                                  (17)

где число Прандтля  определяется по температуре потока пара, а – по температуре стенки; за определяющий размер принять длину плиты вдоль направления потока пара L.

2. Передача теплоты через оребренную поверхность плоской стенки

В условиях стационарной теплопроводности ребра третьего рода распределение температуры в нем для одномерной задачи описывается дифференциальным уравнением:

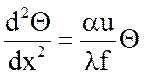                                                          ,                    (18)

где      – коэффициент теплообмена между поверхностью ребра воздухом, ;

          u – периметр ребра, м; ;

          l – коэффициент теплопроводности материала ребра, ;

          f – площадь сечения ребра, м², ;

           – разность между текущей температурой на поверхности ребра и температурой окружающей среды.

Уравнение (18) представим в виде:

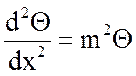                                                           ,                     (19)

где 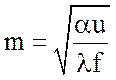     – параметр ребра, .

Выражение (19) представляет собой обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами и имеет решение:

                                                      .                (20)

 Постоянные интегрирования с₁ и с₂ вычислим с помощью граничных усло­вий:

при  

при ,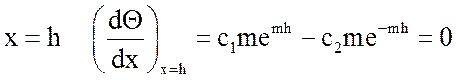

где     t₁ – температура в основании ребра, ;

          h – высота ребра, м.

Тогда частное решение уравнения (19) выразится в виде зависимости тем­пературного напора  от координаты х:

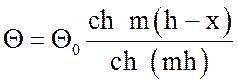                                                   ,              (21)

где      – гиперболические функции,

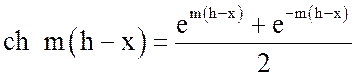                                           ;     (22)

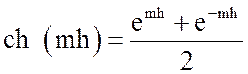                                             .             (23)

Начало координаты х принять в основании ребра.

Тепловой поток, передаваемый через основание ребра, определяется по вы­ражению:

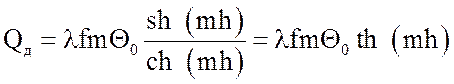                                    .                                                                  (24)

Максимальный тепловой поток, передаваемый ребром, при абсолютной теплопроводности материала ребра  и при температуре по всей поверх­ности ребра, равной температуре в его основании, определиться по формуле:

                                                         .                   (25)