Теоретические основы теплотехники. Тепломассообмен: Задания на курсовое проектирование и методические указания к выполнению, страница 3

Методические указания к выполнению курсовой работы

1. Нестационарная теплопроводность тел

Плита толщиной S, выполненная из однородного материала и ограни­ченная плоскопараллельными поверхностями, по размерам много боль­шими S, подвергается внезапному тепловому воздействию с обеих сторон потоком пара. Процесс нестационарной теплопроводности в плите описы­вается дифференциальным уравнением:

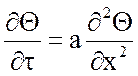                                                           .                       (1)

Считая, что процесс нагрева плиты идет по обе стороны, начало координат целе­сообразно поместить в середине плиты по толщине.

Применительно к условиям одномерной задачи решение уравнения (1) представляется в виде:

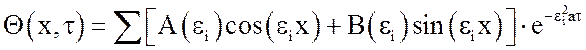                      ,                                                                   (2)

где      – разность температуры в любой точке толщины плиты в любой момент времени и при постоянной температуре потока пара;

           – положительная размерная величина;

           – произвольные постоянные, зависящие от .

Функция  есть нечетная функция, так как при переходе от +х к –х меняется знак этой функции. Функция  для симметрич­ного процесса будет четной. Тогда решение (1) выразится в виде:

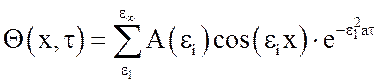                                         .     (3)

 Используя граничное условие третьего рода:

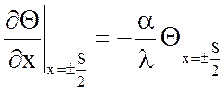                                                    ,                 (4)

для любого частного решения уравнения (3) имеем равенство:

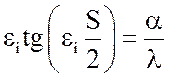                                                        ,                     (5)

где      – коэффициент теплоотдачи от потока пара к поверхности плиты;

          – коэффициент теплопроводности материала плиты.

Обозначив 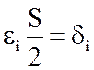 и имея в виду, что 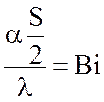, получим:

                                                            .                        (6)

По физическому смыслу Bi есть критерий Био, представляющий собой от­ношение термического сопротивления теплопроводности материала плиты к термическому сопротивлению теплоотдачи от потока пара к плите.

 Трансцендентное уравнение (6) имеет бесконечное множество корней

(). Значения первых пяти корней  даны в табл. 4.

 С учетом (6) решение уравнения (4) представляется в виде:

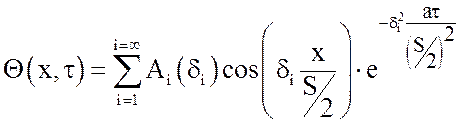                                   .                                                                   (7)

 Безразмерный параметр 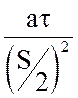 характеризует изменение температуры во времени и называется критерием Фурье:

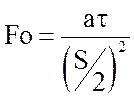                                                           .                       (8)

В начальный момент времени при  имеем уравнение:

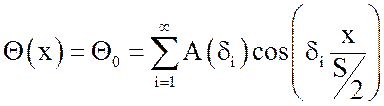                                         ,     (9)

представляющее равномерно быстросходящийся ряд. После интегрирования членов ряда находим постоянные коэффициенты:

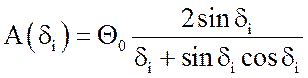                                              .         (10)

 Тогда окончательное решение задачи будет в виде:

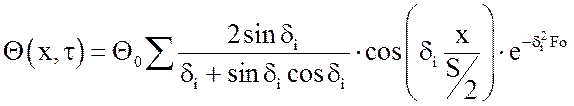                        ,                                                                  (11)

где – начальный температурный напор, .

Таблица 4

Краткая таблица значений корней уравнения (6)

	d1	d2	d3	d4	d5
100,0 60,0 40,0 20,0 10,0 6,0 4,0 2,0 1,0 0,8 0,6 0,4 0,2 0,1 0,01 0,0	1,5708 1,5552 1,5451 1,5325 1,4961 1,4289 1,3496 1,2646 1,0769 0,8603 0,7910 0.7051 0,5932 0,4328 0,3111 0,0998 0,0000	4,7124 4,6658 4,6353 4,5979 4,4915 4,3058 4,1116 3,9352 3,6436 3,4256 3,3744 3,3204 3,2636 3,2039 3,1731 3,1448 3,1416	7,8540 7,7764 7,7259 7,6647 7,4954 7,2281 6,9924 6,8140 6,5783 6,4373 6,4074 6,3770 6,3461 6,3148 6,2991 6,2848 6,2832	10,9956 10,8871 10,8172 10,7334 10,5117 10,2003 9,9667 9,8119 9,6296 9,5293 9,5087 9,4879 9,4670 9,4459 9,4354 9,4252 9,4248	14,1372 13,9981 13,9094 13,8048 13,5420 13,2142 12,9988 12,8678 12,7223 12,6453 12,6296 12,6139 12,5981 12,5823 12,5743 12,5672 12,5664