Расчет сложной цепи постоянного тока, страница 3

Полученная матрица должна быть симметричной. Так можно проверить правильность составления системы уравнений.

Решение системы уравнений (37) с помощью математического редактора Mathсad  (см. прил. 2) дает искомые значения контурных токов:

А;   А; А.

Решение системы уравнений может быть получено и другими методами, например, методом определителей без применения ЭВМ.

Реальные токи  в ветвях цепи находим с учетом направлений протекающих по ветвям контурных токов:

;	(38)	А;
;	(39)	А;
;	(40)	А;
;	(41)	А;
;	(42)	А;
;	(43)	А.

Результаты расчета, полученные методом контурных токов (см. табл. 7), совпадают с результатами расчета по законам Кирхгофа.

 2.2.3. Метод межузлового напряжения является частным случаем метода узловых потенциалов и применяется для расчета электрических цепей с  двумя узлами. В этом случае неизвестными считаются потенциалы узлов.

Чтобы воспользоваться этим методом, преобразуем исходную схему в схему с двумя узлами. Для этого выполним эквивалентное преобразование пассивного «треугольника» сопротивлений R₄, R₅, R₆ в эквивалентную «звезду» r₂, r₃, r₄ (рис. 7, 8):

Индексы сопротивлений полученной «звезды» выбраны по номерам бывших узловых точек, к которым они присоединены в новой схеме. При этом сами точки 2, 3, 4 перестали быть узловыми (см. рис. 8). В схеме, полученной после преобразования, имеется только два узла: старый  (1) и новый (1').

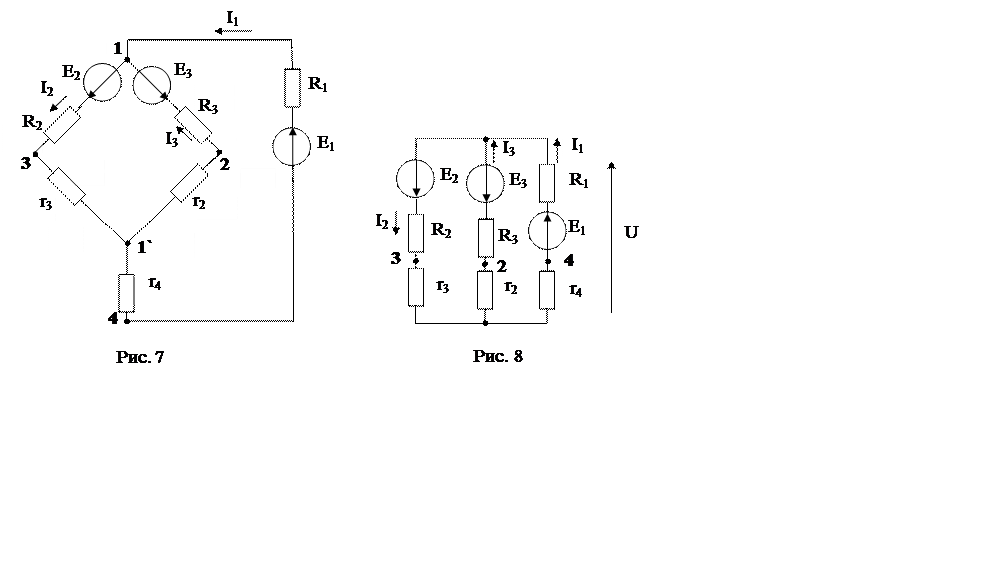
Определяем проводимости оставшихся трех ветвей (индекс указывает на ту ветвь, в которой стоит одноименная ЭДС):

Произвольно выбираем положительное направление напряжения  между узлами 1 и 1' (см. рис. 8) и записываем в соответствии с формализованным правилом расчетное выражение для определения межузлового напряжения. Оно равно алгебраической сумме произведений ЭДС на проводимости соответствующих ветвей, деленной на сумму проводимостей всех ветвей:

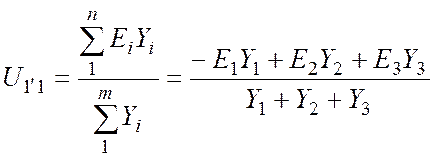 .                              (50)

Знак «плюс» перед слагаемым в числителе ставят, если направления ЭДС и напряжения относительно узлов не совпадают, «минус» – в противном случае. Заметьте, что это правило выбора знака отличается от уже применяемых ранее.

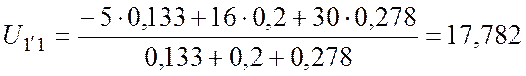  В.

Значения токов в ветвях определяют по второму закону Кирхгофа или используют еще одно формализованное правило: ток в ветви  равен алгебраической сумме действующей в ветви ЭДС и межузлового напряжения, умноженной на проводимость этой ветви:

.                                                 (51)

Знак «плюс» перед ЭДС и напряжением ставится, если ток и ЭДС, ток и напряжение  направлены в одну сторону, в противном случае – знак «минус».

Для рассчитываемой схемы

;	(52)	А;
;	(53)	А;
;	(54)	А.

Полученные значения тока  совпадают с рассчитанными ранее рассмотренными методами, следовательно, расчеты по методу межузлового напряжения выполнены верно.

Листинг расчета рассматриваемой цепи методом межузлового напряжения с помощью математического редактора Mathсad приведен в прил. 2.

2.3. Методические указания к выполнению моделирования

Моделирование режима работы электрической цепи рекомендуется провести в следующем порядке.

2.3.1. Соберите заданную схему и задайте значения параметров элементов. Правила выполнения этих операций приведены в разд. 6. Рационально сначала расположить элементы электрической цепи так, как они показаны на схеме рис. 6, а потом произвести соединения проводниками. При необходимости сопротивления могут быть ориентированы вертикально (рис. 9). Нужно иметь в виду, что в системе схемотехнического моделирования Electronics Workbench невозможно представление диагональных соединений.

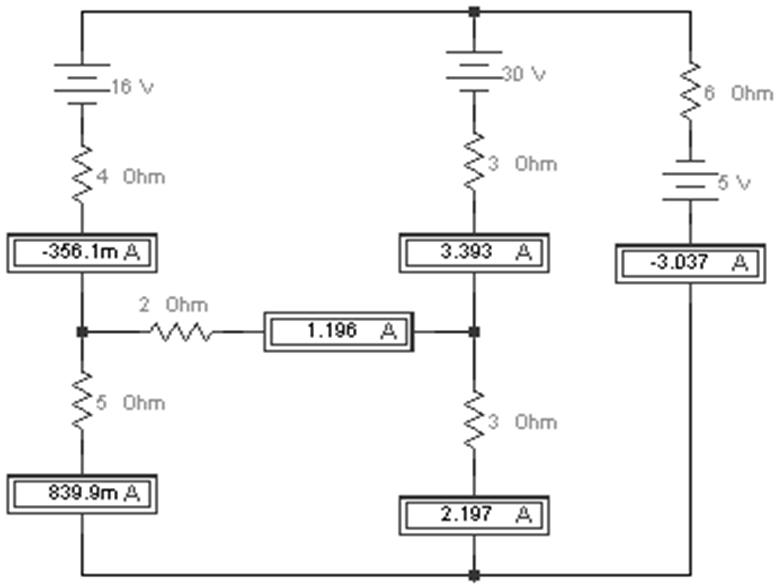Рис. 9

2.3.2. Введите измерительные приборы – индикаторы (амперметры).

2.3.3. Запустите процесс моделирования нажатием переключателя в положение  «I».  Значения измеряемых токов отразятся на приборах-индикаторах. После этого можно остановить процесс моделирования, чтобы ЭВМ не выполняла ненужных вычислений. Занесите значения тока I₁ – I₆  в табл. 7.

2.3.4. На основании полученных данных сделайте вывод о соответствии результатов моделирования и аналитического расчета режима работы схемы.