Электротехника \ Электроника

Расчет сложной цепи постоянного тока, страница 2

3) По первому закону Кирхгофа составляется количество уравнений на одно меньше, чем количество узлов. Для схемы, представленной на рис. 6, количество узлов у = 4. По первому закону Кирхгофа составляем N_I= у –1 = = 3 уравнений.

4) Выбираем любые три узла, например, 1, 2, 3, для которых записываем уравнения по первому закону Кирхгофа:

для узла 1: ; (23)

2: ; (24)

3: . (25)

5) По второму закону Кирхгофа составляется N_II = N – N_I уравнений. В нашем примере N_II = в – (у – 1) = 6 – 3 = 3 уравнения.

6) Выбираем три независимых контура I – III (см. рис. 6) так, чтобы каждый последующий контур содержал хотя бы одну новую ветвь.

7) Принимаем направления обхода контуров I , II – по часовой стрелке, III – против нее.

8) Составляем уравнения по второму закону Кирхгофа.

Для контура I: ; (26)

II: ; (27)

III: . (28)

9) Полная система уравнений будет иметь вид:

;

; (29)

;

10) Решение системы уравнений (29) с помощью математического редактора Mathсad, листинг которой представлен в прил. 2, дает искомые значения тока в ветвях цепи. Знак «минус» указывает на то, что выбранное на схеме направление тока не совпадает с его реальным направлением.

Результаты сведите в табл. 7.

Таблица 7

Значения токов, полученные различными методами

Метод получения результата	Ток, А
Метод получения результата	I₁	I₂	I₃	I₄	I₅	I₆
Расчет по законам Кирхгофа	3,038	-0,356	-3,394	1,196	0,840	-2,198
Расчет методом контурных токов	3,038	-0,356	-3,394	1,196	0,840	-2,198
Расчет методом межузлового напряжения	3,038	-0,356	-3,394	–	–	–
Моделирование	3,037	0,3561	3,393	1,196	0,839	2,197

11) Для проверки правильности расчета составляем баланс мощности:

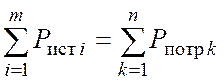. (30)

Для рассматриваемой цепи мощность источников (m = 3)

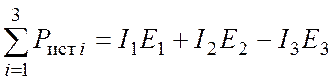, (31)

где мощность источника записывается в балансе со знаком «минус», потому что направление тока и ЭДС не совпадают, источник работает в режиме потребителя.

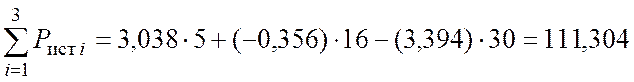Вт.

Мощность приемников (n = 6)

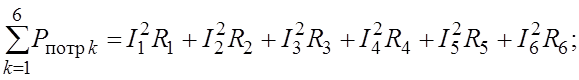(32)

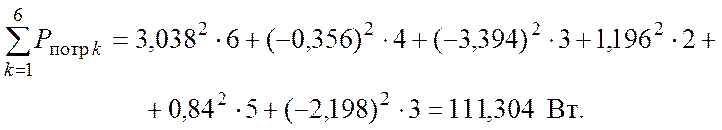
Баланс мощности:

111,304 Вт = 111,304 Вт.

Баланс выполняется, следовательно, расчет токов по законам Кирхгофа выполнен верно.

2.2.2. Метод контурных токов позволяет сократить количество составляемых уравнений и упростить расчеты.

В соответствии с этим методом считается, что в замкнутых контурах протекают так называемые контурные токи J₁, …, J_n. При этом расчетные уравнения составляются по второму закону Кирхгофа. Количество необходимых в этом случае уравнений N_II = в – (у – 1).

Выбор независимых контуров осуществляется так же, как было описано выше. При формировании алгебраической суммы падений напряжения от «протекания» контурных токов учитывают не только падение напряжения на собственных сопротивлениях контура, но и падения напряжения, создаваемые током смежных контуров, протекающим по взаимным сопротивлениям, входящим и в соседние контуры. Ток соседнего контура создает падение напряжения со знаком «плюс», если его направление во взаимном сопротивлении совпадает с направлением рассматриваемого контурного тока, и со знаком «минус» – если не совпадает.

ЭДС в алгебраической сумме принимается со знаком «плюс», если ее направление совпадает с направлением контурного тока, и со знаком «минус» – в противном случае.

После определения контурных токов реальные токи ветвей выражают через контурные токи.

Для проверки правильности расчетов составляется баланс мощности.

Для рассматриваемого примера N_II = в – (у – 1) = 3. Выбираем те же контуры, которые использованы в предыдущем методе, обозначаем направления контурных токов и составляем расчетные уравнения: