Расчет однофазной цепи переменного тока, страница 3

Если на векторной диаграмме сумма векторов токов параллельных ветвей равна вектору  тока в неразветвленной части цепи в соответствии с первым законом Кирхгофа для узловой точки, а сумма векторов напряжения – напряжению источника, то считается, что диаграмма сходится, и это обязательное, но не достаточное условие для вывода о правильности расчетов.

3.2.4. Окончательно о правильности полученных результатов можно судить по балансу мощности, который для цепей переменного тока может быть составлен для комплексов полной мощности источника и потребителей:

 ,                                                     (75)

или для активной и реактивной мощностей как составляющих. Выполним проверку по балансу активной и реактивной мощностей:

;                           ,

(76)

где ,    – угол сдвига фаз между приложенным напряжением и током в неразветвленной части цепи, он зависит от нагрузки цепи и равен аргументу полного комплексного сопротивления ;

      ;

      , где   – действующие значения токов, т. е. модули комплексных чисел, изображающих соответствующие токи;

      , реактивное сопротивление берется с учетом знака.

Активная мощность всегда положительна, реактивная может быть и отрицательной. Знак «минус» указывает на то,  что реактивная мощность отдается цепью в сеть, а не потребляется из сети.

Для рассматриваемого примера:

  Вт;

  Вт;

  вар;

В результате баланс активной мощности:

1297 Вт = 1297 Вт,

а реактивной:

– 1105 вар = – 1105 вар.

Баланс активной и реактивной мощности выполняется, следовательно, расчет однофазной цепи выполнен верно.

3.2.5. Резонанс напряжений в цепи наступает тогда, когда реактивное сопротивление цепи равно нулю. Если реактивное сопротивление цепи носит индуктивный характер (), то необходимо в неразветвленную часть цепи добавить емкостное сопротивление, значение которого равно индуктивной составляющей сопротивления:

                                             (77)

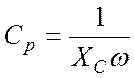.                                                     (78)

Если реактивное сопротивление цепи носит емкостный характер (), то необходимо в неразветвленную часть цепи добавить индуктивное сопротивление:

                                                 (79)

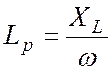.                                                        (80)

В рассматриваемом примере ;  реактивная составляющая сопротивления – емкостная. Рассчитаем индуктивное сопротивление, которое обеспечит в цепи резонанс напряжений:

Ом;

3.3.  Методические указания к выполнению моделирования

Моделирование режима работы однофазной цепи переменного тока рекомендуется провести в следующем порядке.

3.3.1. Соберите заданную схему и задайте значения параметров элементов. Правила выполнения этих операций приведены в разд. 6.

3.3.2. Введите измерительные приборы – индикаторы (амперметры и вольтметр). Выберите в установочных параметрах приборов режим переменного тока (АС). В таком режиме приборы будут показывать действующее значение измеряемых величин. Подключите осциллограф, как показано на рис. 13.

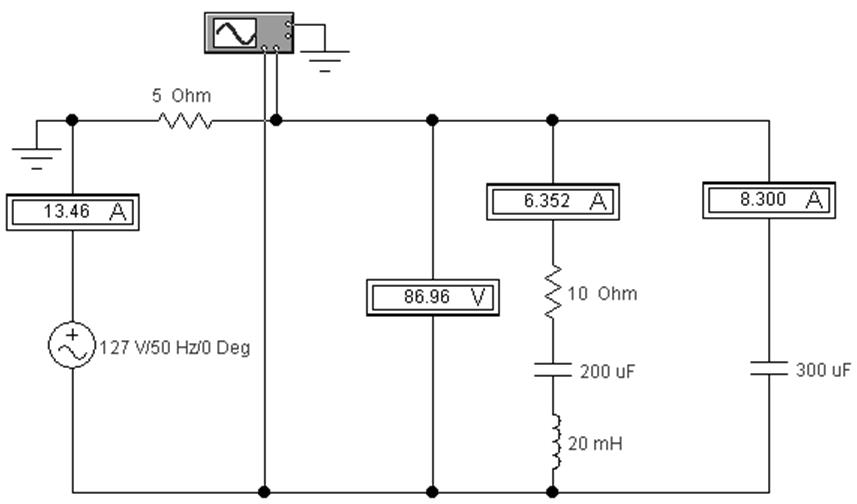Рис. 13

3.3.3. Запустите процесс моделирования нажатием переключателя в положение  «I».  Значения измеряемых величин отразятся на приборах-индикаторах. После этого можно остановить процесс моделирования, чтобы ЭВМ не выполняла ненужных вычислений. Занесите значения тока и напряжения  в табл. 10.

3.3.4. По осциллограмме (рис. 14) рассчитайте угол сдвига фаз между током i₁(t) и напряжением u(t) в соответствии с  выражением:

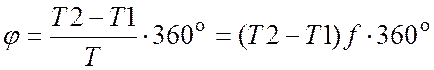,                          (81)

.

3.3.5. Добавьте в неразветвленную часть цепи элемент, создающий резонанс – индуктивность или емкость (рис. 15).

3.3.6. Определите по результатам моделирования действующие значения тока и напряжения в режиме резонанса напряжений (см. рис. 15) и занесите в табл. 10. Проверьте по осциллографу совпадение фаз тока и напряжения в режиме резонанса (рис. 16).

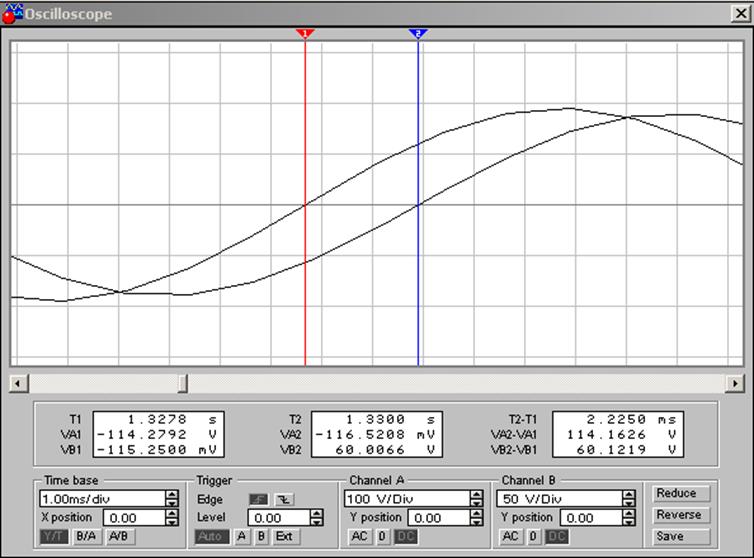
Рис. 14

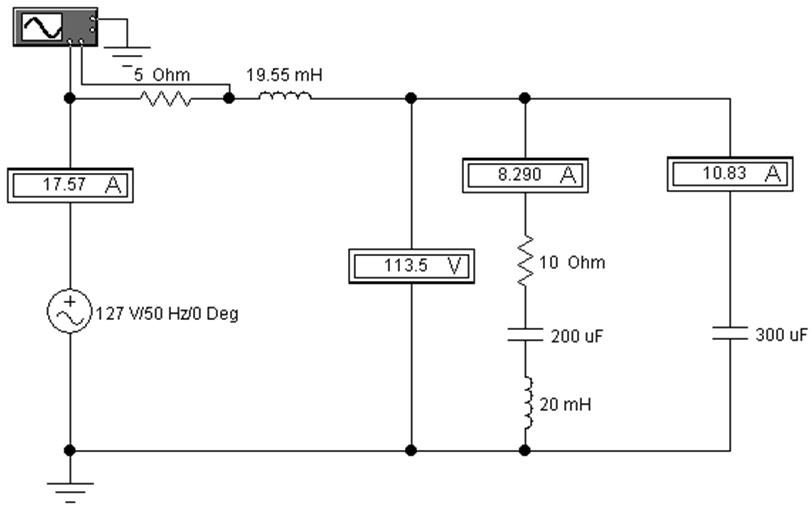
Рис. 15

3.3.7. На основании полученных данных сделайте вывод о соответствии результатов моделирования и аналитического расчета режима работы схемы без резонанса,  и об особенностях работы цепи в режиме резонанса.

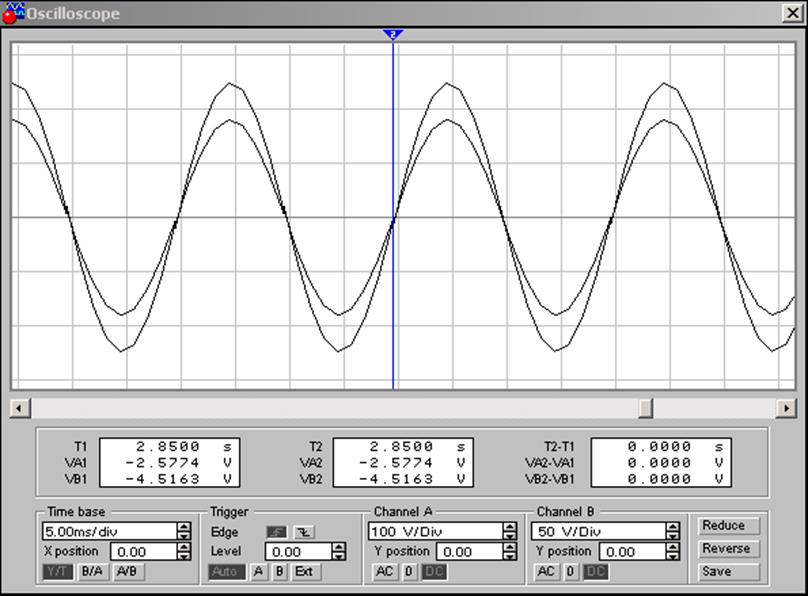
Рис.  16