Расчет однофазной цепи переменного тока, страница 2

Вторая ветвь содержит два реактивных элемента. Общее реактивное сопротивление ветви равно алгебраической сумме индуктивного и емкостного сопротивлений. Знак «плюс» ставится у индуктивного сопротивления, «минус» – у емкостного:

;	(55)	Ом;
;	(56)	Ом;
;	(57)	Ом.

Знак «минус» перед общим реактивным сопротивлением ветви указывает на его емкостный характер. Этот знак сохраняется и при записи полного комплексного сопротивления (см. ниже).

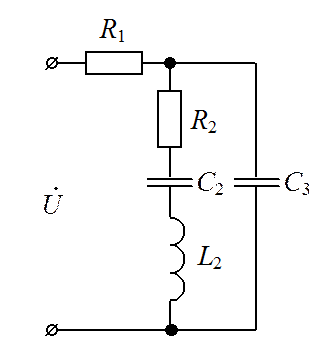
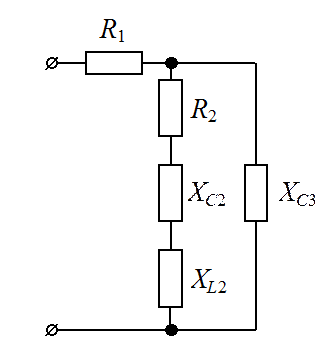
а                                            б

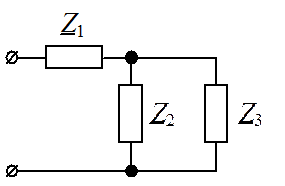
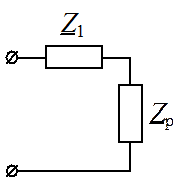
в                                г                     д

Рис. 11

Реактивное сопротивление третьей ветви

;

(58)

Ом.

Полные комплексные сопротивления ветвей в алгебраической, показательной и тригонометрической форме (см. рис. 11) имеют вид:

,                    (59)

где  R – действительная составляющая комплексного сопротивления;

       Х – мнимая составляющая комплексного сопротивления;

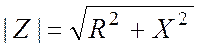     – модуль комплексного сопротивления;

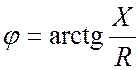         – аргумент комплексного сопротивления, знак аргумента зависит от знака реактивного сопротивления ветви.

Для ветвей рассматриваемой электрической цепи

;                                                 (60)

 Ом;

;                                                 (61)

 Ом;

;                                                   (62)

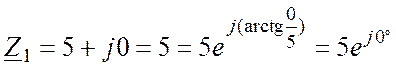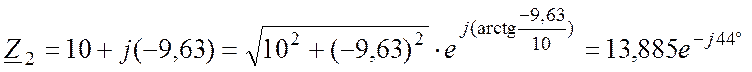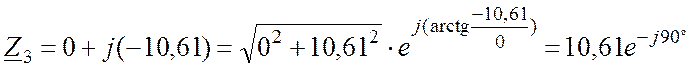 Ом.

Эквивалентная схема с учетом выполненных расчетов представлена на рис.  11, в.

Последующие операции «сворачивания» электрической схемы основаны на рассмотренных в первом разделе свойствах параллельного и последовательного соединений. Нужно помнить, что сложение и вычитание комплексных чисел выполняется в алгебраической форме записи, а умножение и сложение – в показательной, если расчеты ведутся на калькуляторе.

Заменим параллельный участок на эквивалентное сопротивление (рис. 11, г):

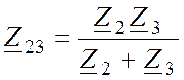;                                                   (63)

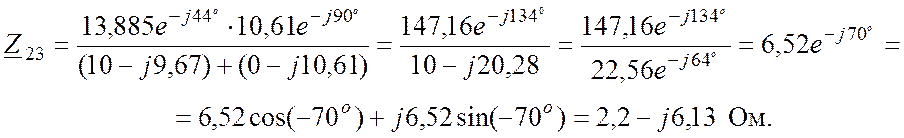
Последовательное соединение двух сопротивлений преобразуем в простейшую цепь (рис.  11, д):

;                                                      (64)

Ом.

Полученная элементарная цепь рассчитывается по закону Ома для цепей переменного тока:

;

(65)

А.

Напряжение на параллельном участке

;

(66)

В.

Токи в параллельных ветвях рассчитываются по выражениям:

;	(67)	А;
;	(68)	А.

Для построения векторной диаграммы необходимо также определить напряжение на неразветвленной части цепи:

;

(69)

В.

Расчет однофазной цепи с помощью математического редактора Mathсad представлен в прил. 3. Нужно заметить, что в Mathсad операции с комплексными числами выполняют в алгебраической форме записи. Для определения модулей и аргументов комплексных чисел нужно выполнить дополнительные команды. Углы в Mathсad вычисляются в радианах. Для перехода в градусную меру измерения углов необходимо дополнительно указать оператор: «deg» (см. прил. 3).

Результаты расчетов занесите в графу «Расчет» табл. 10.

Таблица 10

Полученные значения токов и напряжений для рассматриваемой цепи

Параметр	Действующие значения для исходной схемы		Моделирование  резонанса
	расчет	моделирование
I1, А	13,44	13,46	17,57
I2, А	6,32	6,352	8,290
I3, А	8,26	8,300	10,83
U23, В	87,62	86,96	113,5
φ, градус	40,41	40,05	0

3.2.2. Мгновенные значения тока в ветвях и напряжения можно записать с учетом того, что амплитудное значение тока в  раз больше действующего значения, которое равно модулю полученного комплексного числа:

;	(70)	;
;	(71)	;
;	(72)	;
;	(73)	;
;	(74)	.

3.2.3. Для проверки правильности расчетов строят векторную диаграмму токов и напряжений электрической цепи. Необходимо выбрать масштаб по току , А/мм, и по напряжению , В/мм, построить систему ортогональных осей комплексной плоскости (+1, +j). Векторы тока и напряжения строят из начала координат так, чтобы длина вектора была равна модулю комплексного числа (действующему значению) с учетом масштаба, а угол наклона к действительной оси (+1) – аргументу комплексного числа (начальной фазе), причем положительные углы откладываются против часовой стрелки, отрицательные – по часовой. Векторная диаграмма для рассматриваемого примера приведена на рис. 12.