Методика факторного аналізу. Сутність та види факторного аналізу. Етапи факторного аналізу. Класифікація факторів, страница 5

В інтегральному методі користаються визначеними формулами. Приведемо основні з них для різних моделей.

1. 

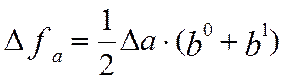
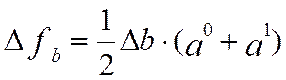
2. 

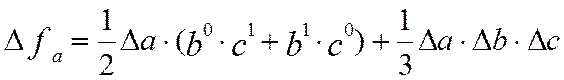
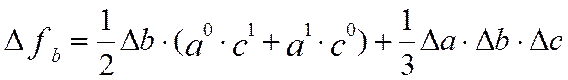
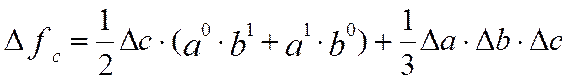
3. 

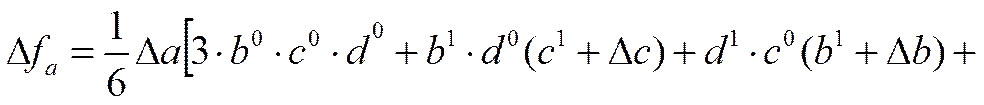
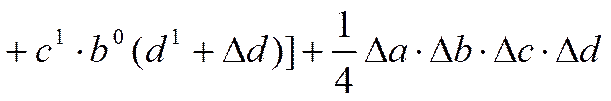
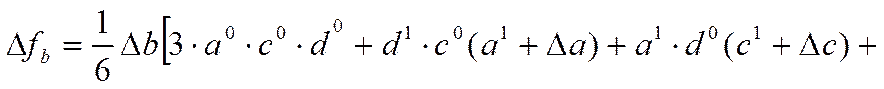
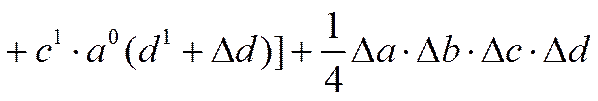
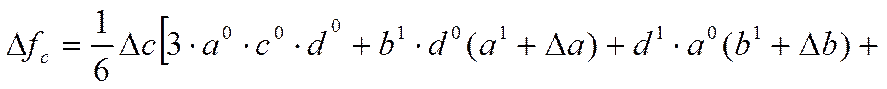
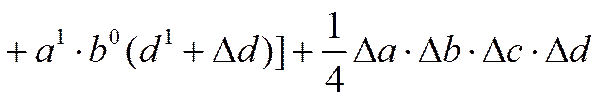
4. 

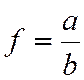
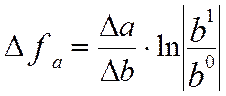
5. 

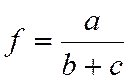
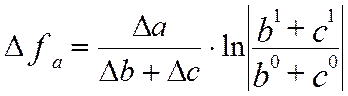
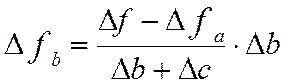
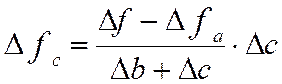
7 Спосіб логарифмування

             Спосіб логарифмування застосовується для виміру впливу факторів у мультиплікативних моделях. Результат розрахунку не залежить від місця розташування факторів у моделі й у порівнянні з інтегральним методом забезпечується більш висока точність у розрахунках. За допомогою логарифмування результат спільної дії факторів розподіляється пропорційно частки ізольованого впливу кожного фактора на рівень результативного показника. У цьому його перевага, а  недолік в обмеженості його застосування. Він застосовується тільки для моделей мультиплікативного типу.

              При логарифмуванні використовуються не абсолютні прирости результативних показників, а індекси їхнього росту (зниження).

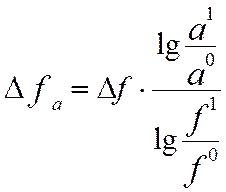
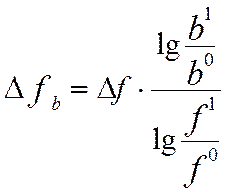
              З формул випливає , що загальний  приріст результативного показника  розподіляється між факторами пропорційно  відношенню логарифмів індексів факторних показників до логарифму індексу результативного показника. При цьому не має значення який логарифм застосовується натуральний або десятичний.

Наведемо приклади застосування методів факторного аналізу

Оцінити абсолютну зміну обсягу випуску товарної продукції (Q) у звітному періоді порівняно з планом під впливом таких факторів, як: середньоспискова чисельність промислово-виробничого персоналу (), середня кількість днів, відпрацьованих одним працівником за рік (Д_Н), середня кількість часів, відпрацьованих одним працівником за день (Час), середньочасова виробітка одного працюючого (ПП). Вихідні дані наведені у таблиці 1.

Таблиця 1 — Показники з праці

Найменування показника	Умовне позначення	Значення		Зміна
		План	Факт	абсолют-на (+/-)	відносна, Тр, %
1. Обсяг випуску товарної продукції, тис. грн.	Q	3850	3875,9	+25,9	100,672
2. Середньоспискова чисельність ПВП, осіб		927	923	-4	99,569
3. Середня кількість днів, відпрацьованих одним працівником ПВП	Дн	298	290	-8	97,315
4. Середня кількість годин, відпрацьованих одним робітником за один день	Час	7,5	7,4	-0,1	98,667
5. Середньогодинний виробіток на одного робітника ПВП, грн.	ППчас	1,858	1,957	+0,099	105,328

Для розв'язання задачі побудуємо аналітичну та графічну модель взаємозв'язку між результативними показником (Q) та факторними.

Середньорічний виробіток одного працюючого (П_Т) можливо знайти як:

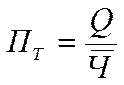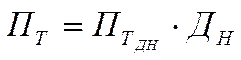; або  (1), (2)

де П_Тдн — середньоденна виробітка одного працюючого.

Деталізуючи показник середньденної виробітки маємо:

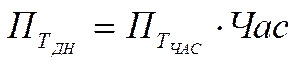 (3)

З формул (1), (2), (3) маємо таку залежність:

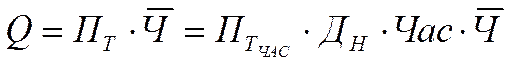 (4)

Графічна модель залежності результативного показника від факторних:

 

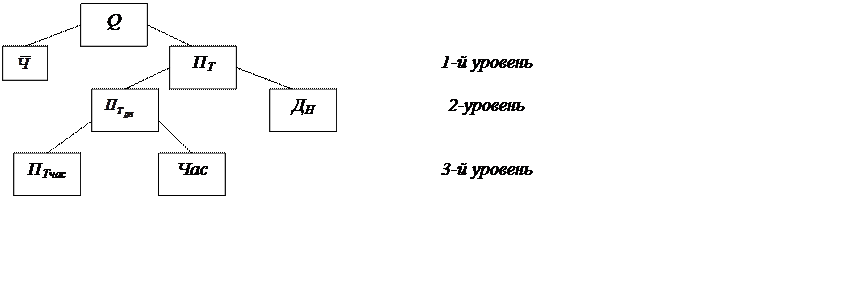Отже маємо багаторівневу модель аналізу.

У моделі ми маємо 3 кількісних фактори та якісний ПП_час — який згідно з правилом будемо оцінювати останнім. Для того, щоб визначити, який з кількісних факторів оцінювати першим застосуємо графічну модель, першими будемо оцінювати вплив факторів 1-го рівня, потім 2-го та 3-го.

Перепишемо формулу (4) у відповідності до порядку оцінки факторів:

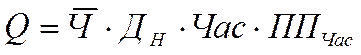 (5)

та застосуємо метод ланцюгових підстав. Оцінимо вплив зміни чисельності працівників ():

          (   )

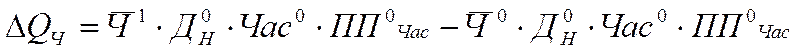 тис. грн.

Оцінимо вплив зміни кількості відпрацьованих днів ():

       (   )

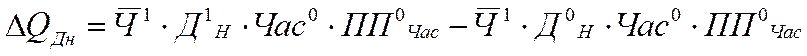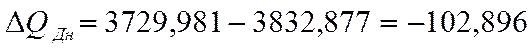 тис. грн.

Оцінимо вплив зміни кількості відпрацьованих за день годин ():

   (   )

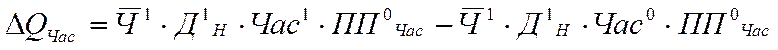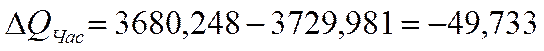 тис. грн.

Оцінимо вплив змін середньогодинного виробітку одного працюючого: