Методика факторного аналізу. Сутність та види факторного аналізу. Етапи факторного аналізу. Класифікація факторів, страница 4

Базова формула	Перетворення	Результат
	розділимо та домножимо 1й член формули на а0
	розділимо та домножимо 1й член формули на а0в0, 2й член на  а0
	Розділимо та домножимо 1й член формули на а0в0с0, 2й член на  а0в0

Таким чином можемо вивести правило застосування методу для моделей мультиплікативного типу.

Для того, щоб визначити вплив на результативний показник першого відповідно до порядку оцінки факторів необхідно базове (планове) значення результативного показника помножити на відносну зміну – коефіцієнт приросту (І_а –1) – відповідного факторного показника.

Для того,  щоб визначити вплив другого, третього, (n^го) фактору необхідно базове (планове) значення результативного показника помножити на добуток індексів  зміни попередніх за порядком аналізу показників та на відносну зміну відповідного факторного показника.

Застосування методу відносних різниць для моделей кратного типу.

Для моделей типу П = , де а – кількісний показник, в – якісний показник, застосовують тіж самі правила, що   і для мультиплікативних моделей:

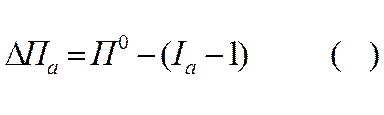
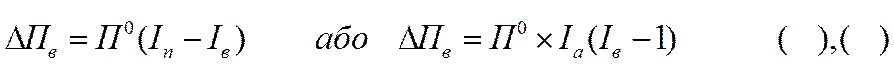
          Для моделей у яких в – кількісний показник, а – якісний показник правило   змінюється і відповідні формули аналізу мають вигляд:

               (     ),(     )

Метод часткової участі

Метод застосовується для змішаних моделей типу П = , де , тобто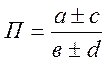

Існує декілька варіантів застосування методу. Опишемо один з них.

Порядок розрахунків.

Для аналізу ми маємо багатоступінчату модель, яку графічно можливо описати:

 

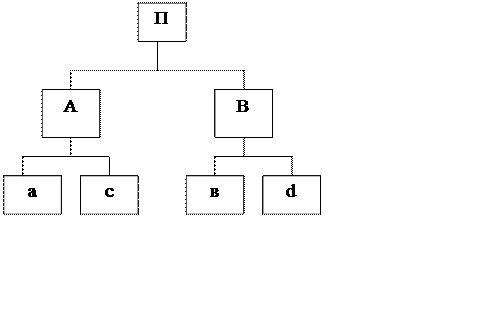Рис. 3 -  Графічна модель аналізу показника

          У таких багаторівневих моделях, по-перше, визначають вплив складних показників на результативний (); по-друге вплив простих факторів на складні ( А_а;   А_с; В_в; В_d); по-третє – визначають вплив простих факторів на складний показник (П_а; П_с; П_в; П_d).

          Для останнього третього етапу визначають відносну зміну складних показників під впливом простих: (А_а;   А_с;  В_в; В_d):

               (   ),     (     )

         (      ),  (     )

          Потім розраховують вплив простих показників на результативний:

                                        (   )

                                        (   )

                                        (   )

                                       (    )

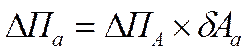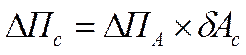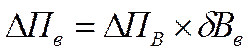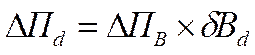6 Інтегральний спосіб

Елімінування як спосіб детермінованого факторного аналізу має істотний недолік. При його використанні виходять з того , що фактори змінюються незалежно друг від друга. Насправді ж вони змінюються спільно, взаємозалежно і від цієї взаємодії виходить додатковий приріст результативного показника, що при застосуванні способів елімінування приєднується до одного з факторів, як правило до останнього. У зв'язку з цим величина впливу факторів на зміну результативного показника змінюється в залежності від місця, на яке поставлений той чи інший фактор у детермінованій моделі. У результаті цього величина впливу одного фактора перебільшується, а іншого - применшується, що викликає неоднозначність оцінки впливу факторів, особливо в тих випадках, коли додатковий приріст досить істотний.

          Щоб позбутися від цього недоліку, у детермінованому факторному аналізі використовується інтегральний метод, що застосовується для виміру впливу факторів у мультиплікативних , кратних і змішаних моделях. Використання цього способу  дозволяє одержувати більш точні результати розрахунку впливу факторів у порівнянні зі способами ланцюгових підстановок, абсолютних і відносних різниць і уникнути неоднозначної оцінки впливу факторів тому, що в даному випадку результати не залежать від місця розташування факторів у моделі , а додатковий приріст результативного показника, що утворився від взаємодії факторів , розкладається між ними пропорційно ізольованому їх впливу на результативний показник.