Решения тестовых задач дисциплины "Линейная алгебра и геометрия"

ТЕСТ №2

                                   ЛИНЕЙНАЯ АЛГЕБРА И ГЕОМЕТРИЯ

№1      Определить ранг матрицы:

     

.

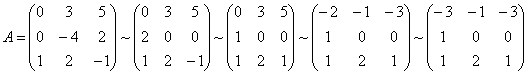
№2      Как изменится длина вектора при ортогональном преобразовании?

Длина вектора при ортогональном преобразовании не изменится, т.к. это следует из определения ортогонального преобразования:

Линейные преобразования (оператор) е  в евклидовом пространстве называется ортогональным, если оно сохраняет скалярное произведение (углы сохраняются и длины тоже), следовательно ортогональный базис переводит в ортонормированный.

№3      Написать разложение вектора x по векторам p,q,r

                        ; ; ;

Решение:

 

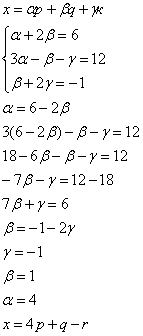
№4      Однородная система, ее общая и фундаментальная система решений.

Рассмотрим произвольную систему линейных однородных уравнений:

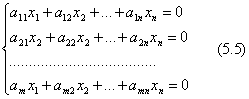
Пусть требуется найти размерность d пространства решений, его базис (фундаментальную систему решений) и общее решение однородной системы линейных уравнений.

Запишем матрицу системы:

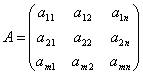
и с помощью элементарных преобразований строк вычислим ранг матрицы. Пусть r(a)=r. Тогда размерность пространства решений есть d=n-r. Если n=r, то однородная система имеет единственное (нулевое) решение. Заметим, что нулевое решение системы (5.5), называется тривиальным решением. Если n>r, то фундаментальная система состоит из n-r линейно независимых решений. Чтобы найти общее решение однородной системы линейных уравнений. Общее решение будет иметь вид:

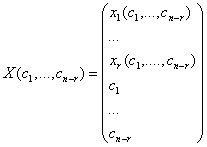
Придавая произвольным постоянным наборы значений (по одной единице, остальные нули), для каждого такого набора решаем систему уравнений и находим соответствующие значения базисных неизвестных. Для каждого набора значений получаем решения , которые линейно независимы. Чтобы убедится, что найденные решения линейно независимы составим матрицу из столбцов и вычислим ее ранг.

Решения  называются базисными и составляют  фундаментальную систему решений однородной системы. С использованием фундаментальной системы общее решение однородной системы линейных уравнений имеет вид:

, где -произвольные постоянные.

№5      Найти точку пересечения прямой и плоскости.

Координаты точки пересечения прямой  (13)

С плоскостью  (14)

Должны одновременно удовлетворять уравнениям (13) и (14) и, чтобы найти эти координаты, надо решить эти уравнения совместно, считая x, y и z неизвестными.

Перейдем от канонических уравнений прямой (13) к параметрическими уравнениям:

   (15)

Подставляя эти выражения для x, y и z в уравнение (14), получим

Откуда:

  (16)

По найденному значению t* из формул (15) получаем координаты искомой точки.