Численные методы интегрирования. Численное решение обыкновенных ДУ

СОДЕРЖАНИЕ

1. Численные методы интегрирования.

2.Численное решение обыкновенных  ДУ.

1.Численные методы интегрирования.

Постановка  задачи:

1. требуется вычислить точное значение интеграла

J₀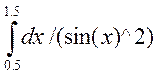₌ =-ctg(1.5)+ctg(0.5)= 1,759573

2.найти J₀ =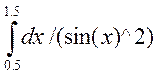 с помощью методов прямоугольников:

J₁ =h и трапеций: J₂  =h((f(x₀ )+f(x_n))/2 + ). Сравнить с точным значением. Рассмотреть для каждого метода два случая:N=10,N=20, N=40.

Формула прямоугольников.

Пусть F(x)=f(x_i-1),х€[x_i-1,x_i],т.е. аппроксимируем f(x)левой кусочно-постоянной интерполяцией. Тогда получим

 ==f(x_i-1)=f(x_i-1 )(x_i-x_i-1)=h*f(x_i).

Таким образом  =h(x_i-1 ). Эта формула называется формулой левых прямоугольников.

Аналогично может быть получена формула правых прямоугольников.

f(x)=f(x_i). в результате получим =h.

Если на каждом отрезке [x_i-1,x_i] заменить значение функции f(x) на ее значение в середине отрезка, т.е.  f(x)=f(x_i-1/2),x€[x_i-1,x_i],получим формулу средних прямоугольников.

 Формула трапеций.

Во всех рассмотренных формулах площадь криволинейной трапеции заменялась на площадь прямоугольников.

В методе трапеций криволинейная трапеция заменяется на прямолинейную ,площадь которой вычисляется по известным формулам:

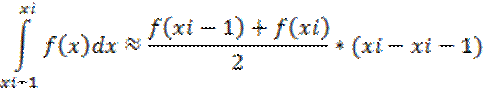
Формула трапеций может быть также получена путем замены подынтегральной функции интерполяционным полиномом первой степени:

L_1,x =1/h[(X-X_i-1)f(X_i)-(X-X_i)f(X_i-1)].

Можно показать ,что формула трапеций совпадает с формулой средних прямоугольников для таблично заданной функции .

Формулу трапеций можно также записать в виде :

.

Результаты вычислений:

а=	0,5	b=	1,5	h=	0,10	N=	10
а=	0,5	b=	1,5	h=	0,05	N=	20
а=	0,5	b=	1,5	h=	0,025	N=	40

i	Xi	f(Xi)	(Xi+Xi+1)/2	f((Xi+Xi+1)/2)	f(i+1)+4*f(i+0.5)+f(i+1)
0	0,50	4,3506853	0,55	3,660296126	22,12842485
1	0,60	3,13655504	0,65	2,73037106	16,46758245
2	0,70	2,40954317	0,75	2,152243696	12,96177575
3	0,80	1,9432578	0,85	1,771723218	10,6598741
4	0,90	1,62972342	0,95	1,511384998	9,087546346
5	1,00	1,41228293	1,05	1,329039557	7,987489687
6	1,10	1,25904853	1,15	1,200281331	7,211323408
7	1,20	1,15114955	1,25	1,110405624	6,669842496
8	1,30	1,07707045	1,35	1,050380369	6,308340146
9	1,40	1,02974822	1,45	1,014734881	6,093716662
10	1,50	1,00502892

i	Xi	f(Xi)	(Xi+Xi+1)/2	f((Xi+Xi+1)/2)	f(i+1)+4*f(i+0.5)+f(i+1)
0	0,50	4,3506853	0,525	3,980662324	23,93363072
1	0,55	3,66029613	0,575	3,381162359	20,32150061
2	0,60	3,13655504	0,625	2,921082697	17,55125689
3	0,65	2,73037106	0,675	2,560841389	15,38327978
4	0,70	2,40954317	0,725	2,27402649	13,65789282
5	0,75	2,1522437	0,775	2,042472872	12,26539298
6	0,80	1,9432578	0,825	1,853360472	11,12842291
7	0,85	1,77172322	0,875	1,697438316	10,1911999
8	0,90	1,62972342	0,925	1,567901609	9,412714857
9	0,95	1,511385	0,975	1,459661349	8,76231332
10	1,00	1,41228293	1,025	1,368857287	8,216751631
11	1,05	1,32903956	1,075	1,292525991	7,758192053
12	1,10	1,25904853	1,125	1,228370225	7,372810765
13	1,15	1,20028133	1,175	1,174596018	7,049814957
14	1,20	1,15114955	1,225	1,129795893	6,780738748
15	1,25	1,11040562	1,275	1,092864204	6,558932887
16	1,30	1,07707045	1,325	1,062935228	6,379191728
17	1,35	1,05038037	1,375	1,039337696	6,237479373
18	1,40	1,02974822	1,425	1,021561466	6,130728965
19	1,45	1,01473488	1,475	1,009233374	6,056697291
20	1,50	1,00502892