Новосибирский Государственный
Архитектурно-строительный университет.
(Сибстрин)
кафедра прикладной математики
Лабораторная работа №1.
Решение нелинейных алгебраических уравнений.
Часть 1.
Выполнила: Задорожный И.Е.
Группа 328 ПГС
Проверила: Федорченко И.А.
Новосибирск 2010
Содержание:
1. Постановка задачи
2. Исследование уравнения
3. Описание методов решения
4. Результаты расчетов
5. Вывод
1. Постановка задачи.
Задано нелинейное алгебраическое уравнение f(x)=0. Решением уравнения является значение х*, такое, что f(x*)=0. Решить уравнение приближённым (итерационным) методом – значит построить последовательность {xn} (n – номер итерации, т.е. приближения к решению), сходящуюся к точному решению уравнения: limxn =x*. Итерационный метод задаётся рекуррентной формулой, позволяющей определить последующее приближение по известным предыдущим. Итерационный процесс заканчивается, когда |xn-x*|<ε, где ε-точность метода, некоторое наперёд заданное число. Перед тем, как начать решение уравнения итерационным методом, необходимо исследовать уравнение на наличие корней и для каждого из корней найти свой интервал изоляции [a,b], содежащего единственный корень уравнения. Условием того, что на отрезке [a,b] существует хотя бы один корень уравнения является f(a)f(b)<0.
Задано нелинейное алгебраическое уравнение:
![]()
2. Исследование уравнения.
Для исследования уравнения используют следующие методы: аналитический, графический и табличный. В настоящей работе функцию будем исследовать с помощью табличного и графического способов.
2.1 Табличный способ: 2.2 Графический способ:
a=-10; b=10; d=0,5; ε=0.001
|
x |
F(x) |
|
-10 |
869 |
|
-9,5 |
581,3273 |
|
-9 |
381 |
|
-8,5 |
242,2887 |
|
-8 |
147 |
|
-7,5 |
82,26934 |
|
-7 |
39 |
|
-6,5 |
10,75967 |
|
-6 |
-7 |
|
-5,5 |
-17,4952 |
|
-5 |
-23 |
|
-4,5 |
-25,1226 |
|
-4 |
-25 |
|
-3,5 |
-23,4363 |
|
-3 |
-21 |
|
-2,5 |
-18,0931 |
|
-2 |
-15 |
|
-1,5 |
-11,9216 |
|
-1 |
-9 |
|
-0,5 |
-6,33579 |
|
0 |
-4 |
|
0,5 |
-2,04289 |
|
1 |
-0,5 |
|
1,5 |
0,603553 |
|
2 |
1,25 |
|
2,5 |
1,426777 |
|
3 |
1,125 |
|
3,5 |
0,338388 |
|
4 |
-0,9375 |
|
4,5 |
-2,70581 |
|
5 |
-4,96875 |
|
5,5 |
-7,7279 |
|
6 |
-10,9844 |
|
6,5 |
-14,739 |
|
7 |
-18,9922 |
|
7,5 |
-23,7445 |
|
8 |
-28,9961 |
|
8,5 |
-34,7472 |
|
9 |
-40,998 |
|
9,5 |
-47,7486 |
|
10 |
-54,999 |
2.2 Графический способ:
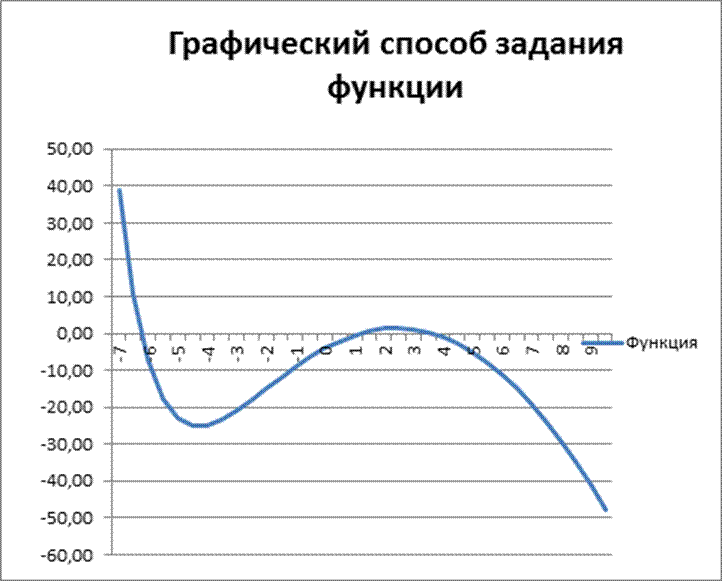
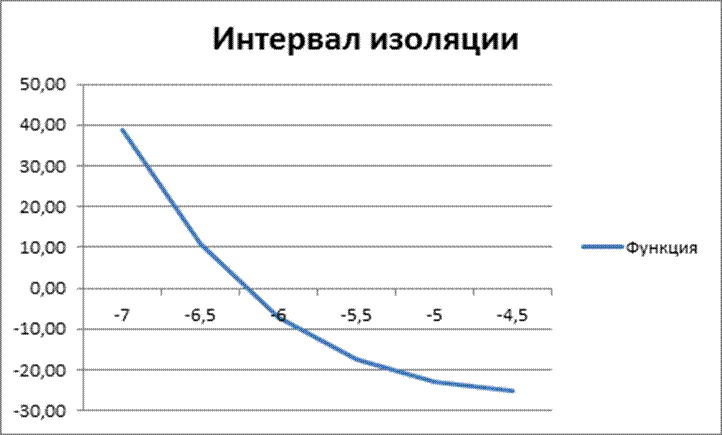
2.3 Интервалы изоляции корней уравнения:
1. [-6,5;-6]
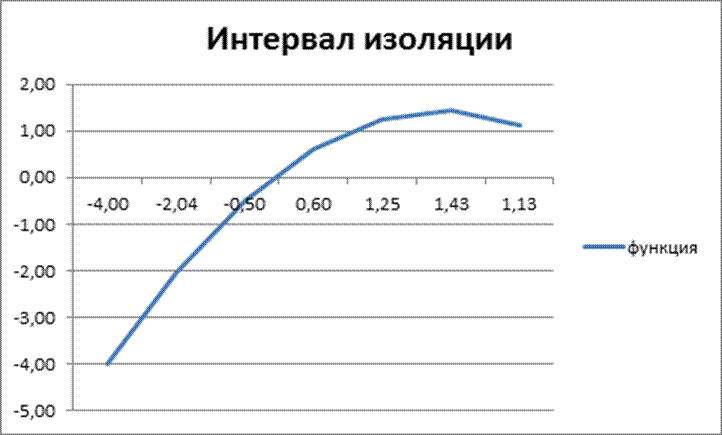
2. [1;1,5]
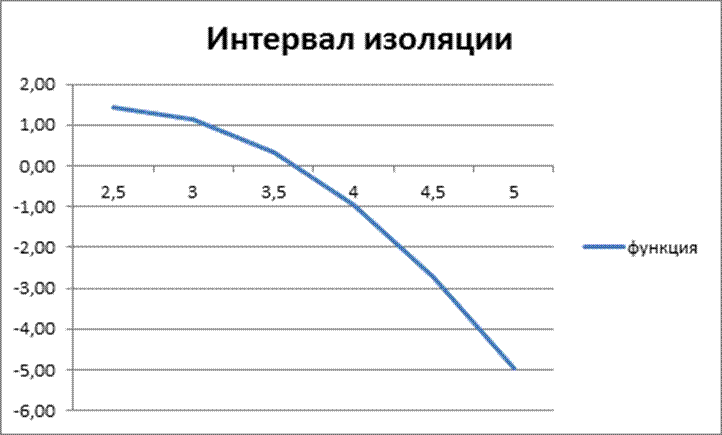
3. [3,5;4]
3. Описание методов решения.
После того, как интервалы изоляции построены, можно решить уравнение с помощью приведенного ниже метода.
3.1 Метод хорд. Если f”(a) f(а)<0, то положим х0=а. Следующие интерации определяются по формуле: хк+1=хк-[(b-хк)/(f(b)-f(хк))]*f(хк). В случае f”(a) f(а)>0, то х0=b., а следующие интерации находим по формуле: хк+1=а-[(хк-а)/(f(хк)-f(а))]*f(а). Окончание интерационного цикла в этои методе происходит по условию: |F(хк )|<ε.
4. Результаты расчетов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.