МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (СИБСТРИН)
Кафедра прикладной математики
Лабораторная работа № 1
Решение нелинейных алгебраических уравнений.
Методы решения систем линейных алгебраических уравнений
Вариант 4
Выполнила: студентка 321гр.
Волкова М. О.
Проверила: Федорченко И. А.
Новосибирск 2010
Часть № 1 : Решение нелинейных алгебраических уравнений
Постановка задачи
Задано
нелинейное алгебраическое уравнение![]() . Решением уравнения
является значение х*, такое, что
. Решением уравнения
является значение х*, такое, что![]() .
Решить уравнение приближенным (итерационным) методом – значит построить
последовательность {xn}
(n – номер итерации, т.е.
приближения к решению), сходящуюся к точному решению уравнения:
.
Решить уравнение приближенным (итерационным) методом – значит построить
последовательность {xn}
(n – номер итерации, т.е.
приближения к решению), сходящуюся к точному решению уравнения: ![]() . Итерационный метод задается рекуррентной
формулой, позволяющей определить последующее приближение по известным
предыдущим. Итерационный процесс заканчивается, когда
. Итерационный метод задается рекуррентной
формулой, позволяющей определить последующее приближение по известным
предыдущим. Итерационный процесс заканчивается, когда ![]() ,
где ε – точность метода, некоторое наперед заданное число. Перед тем, как
начать решение уравнения итерационным методом, необходимо исследовать уравнение
на наличие корней и для каждого из корней найти свой интервал изоляции [a,b],
содержащего единственный корень уравнения. Условием того, что на отрезке [a,b]
существует хотя бы один корень уравнения, является f(a)f(b)<0.
,
где ε – точность метода, некоторое наперед заданное число. Перед тем, как
начать решение уравнения итерационным методом, необходимо исследовать уравнение
на наличие корней и для каждого из корней найти свой интервал изоляции [a,b],
содержащего единственный корень уравнения. Условием того, что на отрезке [a,b]
существует хотя бы один корень уравнения, является f(a)f(b)<0.
Задание
Дано: ![]()
Требуется:
- исследовать уравнение табличным и графическим способом, найти интервалы изоляции для всех корней;
-
для
каждого интервала изоляции с заданной точностью ![]() найти корни уравнения с
использованием метода деления отрезка пополам, метода Ньютона и метода секущих;
найти корни уравнения с
использованием метода деления отрезка пополам, метода Ньютона и метода секущих;
-
для
одного из корней проследить изменение количества итераций, необходимых для
решения уравнения с точностью ![]()
- сравнить все методы по количеству итераций.
Исследование уравнения
Табличный
способ – это построение таблицы , состоящей из столбца
аргумента х и столбца значений функции ![]() . О
наличии корней свидетельствуют перемены знака функции. Чтобы не произошла
потеря корней, шаг изменения аргумента должен быть достаточно мелким, а
интервал изменения достаточно большим.
. О
наличии корней свидетельствуют перемены знака функции. Чтобы не произошла
потеря корней, шаг изменения аргумента должен быть достаточно мелким, а
интервал изменения достаточно большим.
В интервале от -4 до 2 с шагом 0,2 вычислим значения функции и результаты представим в виде таблицы:
|
х |
|
|
-4 |
-6 |
|
-3,8 |
-4,8033 |
|
-3,6 |
-3,6912 |
|
-3,4 |
-2,66489 |
|
-3,2 |
-1,7257 |
|
-3 |
-0,875 |
|
-2,8 |
-0,11428 |
|
-2,6 |
0,554984 |
|
-2,4 |
1,131316 |
|
-2,2 |
1,613366 |
|
-2 |
2 |
|
-1,8 |
2,290446 |
|
-1,6 |
2,484485 |
|
-1,4 |
2,582701 |
|
-1,2 |
2,586796 |
|
-1 |
2,5 |
|
-0,8 |
2,327583 |
|
-0,6 |
2,077511 |
|
-0,4 |
1,761257 |
|
-0,2 |
1,394822 |
|
0 |
1 |
|
0,2 |
0,605948 |
|
0,4 |
0,251121 |
|
0,6 |
-0,01434 |
|
0,8 |
-0,1257 |
|
1 |
3,33E-13 |
|
1,2 |
0,468251 |
|
1,4 |
1,412471 |
|
1,6 |
3,000469 |
|
1,8 |
5,442335 |
|
2 |
9 |
Из таблицы видно, что смена знака функции происходит три раза на интервалах [-2,8; -2,6], [0,4; 0,6], [0,8; 1,2]. Эти интервалы можно выбрать в качестве интервалов изоляции корней.
Графический
способ – построение графика функции ![]() и определение числа корней по количеству
пересечений графика с осью х.
и определение числа корней по количеству
пересечений графика с осью х.
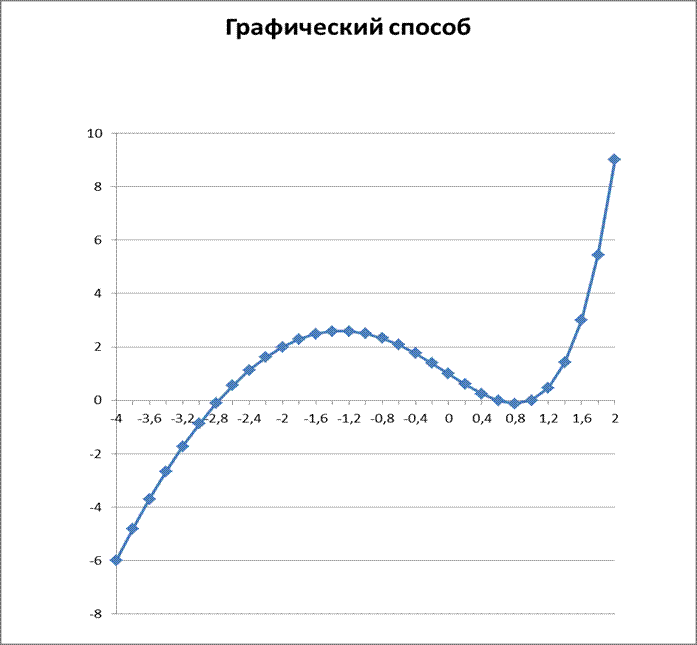
Из графика следует, что интервалы изоляции корней могут быть выбраны следующим образом: [-2,8; -2,6], [0,4; 0,6], [0,8; 1,2].
Решение НАУ приближенными (итерационными) методами
Метод деления отрезка пополам (дихотомии)
Идея заключается в делении отрезка пополам, на котором содержится корень, по тех пор, пока не будет достигнута заданная точность.
Поделим
отрезок [a, b]
пополам. Координата середины отрезка определится как 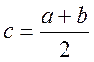 .
Теперь корень остался на одной из частей: [a,
c] или [c,
b]. Если
.
Теперь корень остался на одной из частей: [a,
c] или [c,
b]. Если ![]() , то это говорит о том, что функция на
отрезке [a, c]
меняет свой знак, т. е. на данном интервале находится корень. В этом случае
деление отрезка можно повторить, приняв в качестве нового правого конца точку с,
т. е. приняв в=с. В противном случае корень попал на половину [c,
b], и необходимо
изменить значение левого отрезка: а=с. Поскольку корень всегда заключен
внутри отрезка, итерационный процесс можно остановить, если длина отрезка станет
меньше заданной точности
, то это говорит о том, что функция на
отрезке [a, c]
меняет свой знак, т. е. на данном интервале находится корень. В этом случае
деление отрезка можно повторить, приняв в качестве нового правого конца точку с,
т. е. приняв в=с. В противном случае корень попал на половину [c,
b], и необходимо
изменить значение левого отрезка: а=с. Поскольку корень всегда заключен
внутри отрезка, итерационный процесс можно остановить, если длина отрезка станет
меньше заданной точности ![]() .
.
Метод Ньютона (касательных)
Метод
Ньютона определяется формулой: 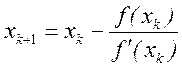 . Суть метода состоит в
замене нелинейной функции
. Суть метода состоит в
замене нелинейной функции ![]() линейной, которую можно
с легкостью решить.
линейной, которую можно
с легкостью решить.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.