Проверка статистической значимости коэффициентов и общего качества уравнения линейной регрессии

Лабораторная работа №3

Проверка статистической значимости коэффициентов и общего качества уравнения линейной регрессии.

1.  Задание: для данных из лабораторной работы №1, проверитьстатистическую значимость коэффициентов линейной регрессии и общее качество линейной модели.

2.  Для нахождения коэффициентов линейной регрессии (ячейкиC12, D12)  и коэффициента детерминации R² (ячейка D14) воспользовались расчетами, выполненными в лабораторных работах 1, 2.

3.  Формулы для анализа значимости коэффициентов b₁, b₀ и общего качества линейной модели приведены на рисунке:

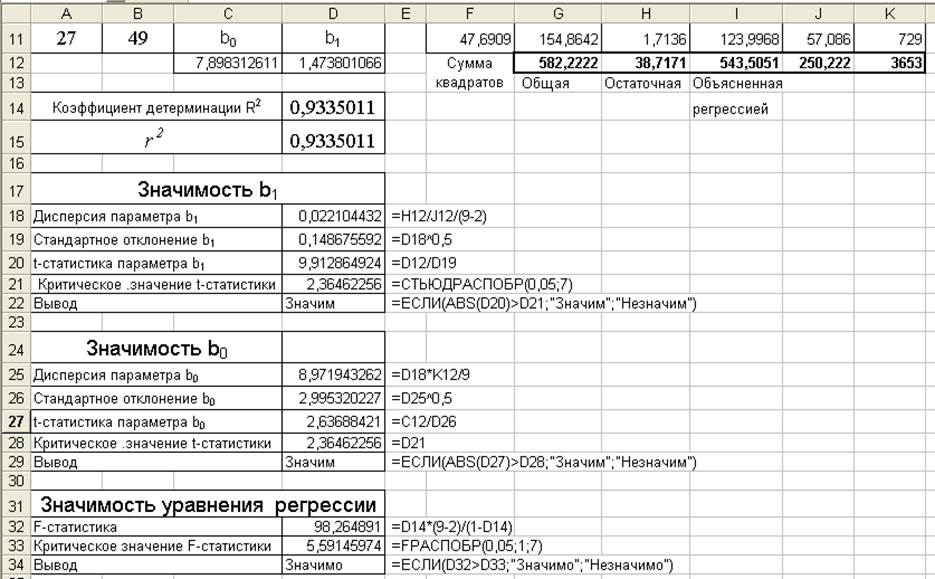
4.  Критическое значение критерия Стьюдента при уровне значимости α = 0,05  t_кр= 2,3646 находим с помощью статистической функции СТЬЮДРАСПОБР.

5.  Сделать вывод о значимости коэффициентов.  Так как наблюдаемые значения критерия Стьюдента для каждого коэффициента больше критического значения, то коэффициенты  b₀ и b₁ статистически значимы.

6.  Критическое значение критерия Фишера при уровне значимости a=0,05  F_кр=F(0,05; 1; 7)=5,5916 находим с помощью функции FРАСПОБР и сравниваем с наблюдаемым значением критерия Фишера F_набл = 50,82. Так как наблюдаемое значение критерия Фишера  больше  критического значения  F_кр,  то найденное уравнение статистически значимо (адекватно).

7.  Провести анализ проделанного:

Проделанный статистический анализ показывает, что в рассматриваемой фирме объем производства  y(тыс. ед.)  зависит от численности занятых x (тыс. чел.) по линейному закону  . При этом все коэффициенты уравнения статистически значимы, а само уравнение адекватно. Так как R²»0,93, полученное уравнение регрессии на 93% объясняет влияние количества занятых x(тыс. чел.)  на изменение объема производства y (тыс. ед.).