Конечно-разностный метод решения одномерных параболических уравнений

Лабораторная работа № 10

Тема: Конечно-разностный метод решения одномерных параболических уравнений.

Для уравнения

                                                                      (1)

k²- const, 0 < x <1, 0 < t < T.

поставим краевую задачу.

Начальные условия возьмем в виде:

u(x,0)=m(x), 0£ x £1.                                                                        (2)

Граничные условия в одном из трех видов:

u(0,t)=m₁(t), u(1,t)=m₂(t),                                                                   (3)

или

u_x(0,t)=m₁(t), u_x(1,t)=m₂(t),                                                                 (4)

или

u(0,t)+a₁u_x(0,t)=m₁(t),

u(1,t)+a₂u_x(1,t)=m₂(t).                                                                      (5)

Задание:

1)   Для поставленной задачи построить тест. В качестве точного решения взять функцию из таблицы 1.

Коэффициент k² и функцию f(x,t) выбирают так, чтобы соответствующая u(x,t)  была точным решением краевой задачи 1, 2 и 3 рода (начальные и краевые условия строят по выбранному точному решению). Поставить все три краевые задачи.

2)   По явной схеме провести расчеты и сравнить результат с точным решением в узлах сетки при h=1/10, h=1/20, h=1/50, h=1/100.

a)   t выбрать из условия выполнения необходимого спектрального признака устойчивости, показать сходимость;

b)   t выбрать так, чтобы не выполнялся необходимый спектральный признак устойчивости.

3)   Провести расчеты по чисто неявной схеме. Результаты сравнить с точным.

a)   h=0,1; t=0,1;  0,05;  0,01,

b)   h=0,01; t=0,1;  0,05;  0,01.

4)   Посчитать до Т=1. Результаты выдать на печать в виде таблице при t_n=n*0,1, n=0, 1, …,10.

5)   Исследовать на устойчивость с помощью гармонического анализа и проверить аппроксимацию схемы “крест” Ричардсона:

.

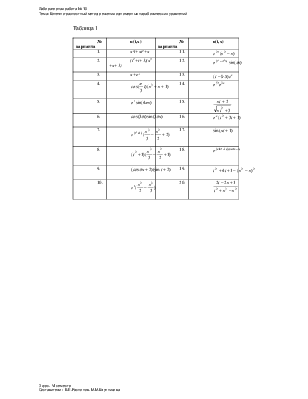
Таблица 1

№ варианта	u(t,x)	№ варианта	u(t,x)
1.	x2t+xt2+x	11.
2.	(t2+t+1)(x3+x+1)	12.
3.	x+e-t	13.
4.		14.
5.		15.
6.		16.
7.		17.
8.		18.
9.		19.
10.		20.