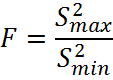
Полученное значение сравнивается с табличным
значением и если выполняется ![]() , то дисперсия считается однородной.
, то дисперсия считается однородной.
После построения математической модели необходимо провести ее проверку на адекватность.
Для этого рассчитывается дисперсия адекватности модели:
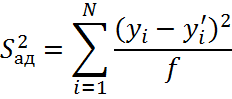
f=N-(k+1)
![]() – среднее значение параметра
оптимизации
– среднее значение параметра
оптимизации
![]() - значение параметра оптимизации,
полученное по математической модели
- значение параметра оптимизации,
полученное по математической модели
f – число степеней свободы
k – количество факторов варьирования
адекватность модели так же оценивается по критерию Фишера, который определяется по формуле:
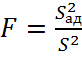 - сравнивается с табличным
значением и если табличное значение больше расчета модель считается адекватной.
- сравнивается с табличным
значением и если табличное значение больше расчета модель считается адекватной.
Табличное значение критериев Фишера определяется по числу степеней свободы, для которых рассчитывается дисперсия.
В 1 случае для оценки однородности модели число степеней свободы:
![]()
Во втором случае при оценке критериев Фишера однородности модели столбцы таблицы определяется значением:
![]() строки таблицы определяют число
степеней свободы
строки таблицы определяют число
степеней свободы ![]() .
.
После проверки адекватности модели проводят оценку значимости каждого коэффициента модели.
Для этого рассчитывают дисперсию коэффициента регрессии по следующей формуле:
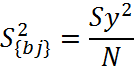
На основе полученной дисперсии строят доверительный интервал
![]()
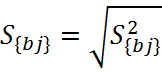
t – коэффициент
Стьюдента – это табличное значение выбирается для числа степеней свободы, при
котором рассчитывается ![]()
![]() – квадратичная ошибка коэффициента
регрессии
– квадратичная ошибка коэффициента
регрессии
Оценка значимости коэффициента модели проводится следующим образом, если его абсолютное значение каждого коэффициента математической модели доверительного интервала это свидетельствует, что коэффициент модели значим.
Чем больше численное значение данного коэффициента, тем сильнее влияние фактора которому соответствует данный коэффициент.
Знаки коэффициентов модели показывают влияние факторов на параметры оптимизации. Если коэффициент положительный, то увеличение значения данного фактора ведет к увеличению параметра оптимизации. Если коэффициент имеет отрицательное значение, то увеличение значения данного фактора ведет к уменьшению значения параметра оптимизации.
Задание для практической работы №6
1. Записать исходные данные для расчетов и определить число полных опытов факторного эксперимента.
2. Определить верхний, нижний и основной уровни варьирования каждого фактора.
3. Составить матрицу планирования эксперимента для заданного количества факторов.
4. Построить линейную модель ОУ в общем виде.
5. Рассчитать все коэффициенты модели.
6. Определить среднее арифметическое результатов экспериментальных данных.
7. Определить значение параметра оптимизации по полученной математической модели.
8. Произвести оценку однородности модели. Рассчитать дисперсию выходной величины и среднеквадратическое отклонение.
9. Произвести оценку адекватности модели, рассчитав дисперсию адекватности.
10. Сделать выводы об адекватности дисперсии и адекватности математической модели.
11. Произвести расчет дисперсий коэффициентов регрессии и определить доверительный интервал.
12. Провести оценку значимости коэффициентов и сделать выводы.
13. Сделать выводы о влиянии каждого соответствующего этим коэффициентам фактора на значении параметра оптимизации.
14. Построить график ( на одной диаграмме)
· Среднее значение параметра оптимизации
· Значение параметра оптимизации по математической модели (будет зависить от количества опытов)
· Значения вертикальной и нижней границ доверительного интервала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.