Определение числа и условий проведения опытов, страница 6

Под планирование понимают определение числа и условий проведения опытов необходимых для достижения поставленной задачи с требуемой точностью.

Как правило, все важные характеристики САУ являются случайными величинами (т.к. САУ подвержено влиянию внешних воздействий). Основной задачей исследований является оптимизация, заключающаяся в нахождении значений совокупно варьируемых параметров системы, при которых целевая функция (выходная величина) принимает экстремальное значение.

Под математической моделью системы понимают уравнения связывающие параметр оптимизации с факторами варьирования (факторами являются переменные величины соответствующие способам воздействия внешней среды на САУ либо на изучаемый объект). Границы изменения факторов определяются, т.о. чтобы обеспечить условия физической реализации процесса.

Факторы должны быть управляемыми (устанавливать на любом уровне независимо друг от друга) и однозначными. Полный факторный эксперимент целесообразно проводить, если он не продолжителен во времени и число варьируемых факторов мало.

Алгоритм получения факторной линейной модели:

Для каждого включенного в эксперимент фактора устанавливают 2 уровня: верхний и нижний.

Верхний:

Нижний:

Среднеарифметическое:

 

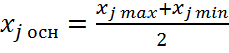
Для полного факторного  эксперимента, в котором реализуются все возможные сочетания факторов, число опытов определяется по формуле:

, где k – число факторов

Далее составляется матрица планирования эксперимента, при этом вводятся обозначения: «+» верхнего уровня варьирования, «-» нижнего уровня, «0» основного уровня.

№	х1	х2	у
1	-	-	у1
2	+	-	у2
3	-	+	у3
4	+	+	у4

Свойства матрицы планирования

1.  Матрица является симметричной относительно центра эксперимента:

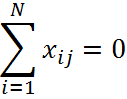
N – число полных опытов

i – номер фактора

j – изменяется от 1 до k

2.  Должно выполняться условие нормировки:

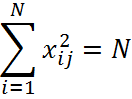
Линейное уравнение математической модели

y – параметр оптимизации (целевая функция)

Для движения к оптимальной точке необходимо вычислить коэффициенты линейной модели по следующему выражению:

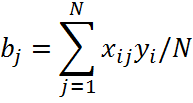
Следует учесть, что  - есть среднеарифметическое значение параметра оптимизации.

При расчетах коэффициентов так же используются кодированные значения  факторов варьирования, которые определяются по следующей формуле:

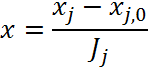
x – кодированное значение факторов

 - натуральное значение факторов

 - натуральное значение основного уровня фактора

интервал варьирования данного фактора

В результате проведения полного эксперимента для каждой строки матрицы варьирования должно быть проведено несколько параллельных опытов. Вследствие чего можно выявить ошибку опытов, которая может быть определена по следующим показателям:

1.  Среднее арифметическое результатов экспериментов (обозначим g)

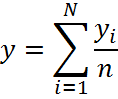
n – число параллельных опытов

2.  Определяется дисперсия

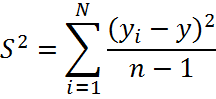
Дисперсия – это среднее значение квадрата отклонение параметра оптимизации от своего среднего значения.

n – число параллельных опытов

n – 1 -  число степеней свободы

 - квадратичная ошибка или среднее квадратичное отклонение (СКО)

Полученные дисперсии проверяют на однородность – это означает, что среди всех полученных дисперсий нет ни одной такой, которая бы значительно превышала все остальные.

Проверка дисперсии на однородность будем проводить при помощи критерия Фишера, который представляет собой отношение >k<