Исследования системы регулирования энергоблока паровой котел – турбина, страница 4

х(t)           g        (t)                             g(t)                           y(t)

ЛЧ

НЭ

Рисунок 10 -  Преобразованная структурная схема нелинейной системы

Передаточная функция линейной части:

                                          

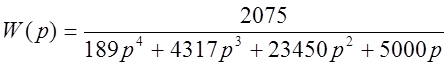
Метод фазовых портретов предназначен для анализа нелинейных систем не выше второго порядка. Преобразуем передаточную функцию линейной части.

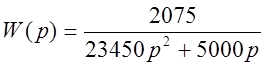
2.2  Построение фазового портрета и переходного процесса

На основании передаточной функции запишем дифференциальное уравнение линейной части системы:

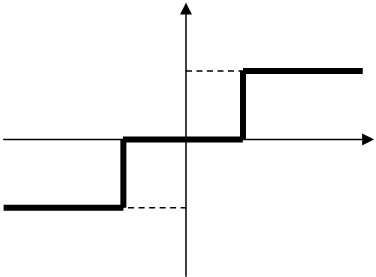
Нелинейный элемент представляет собой  элемент со статической характеристикой в виде релейной характеристики с зоной нечувствительности (рисунок 11).

 

с

     -b                  b

-с

          Рисунок 11 - Статическая характеристика реле

Уравнение нелинейного элемента:

Запишем уравнение сравнивающего элемента:

Предположим, что задающее воздействие . Тогда уравнение нелинейной САУ будет иметь следующий вид:

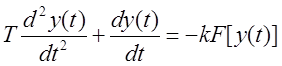
Характеристика нелинейного элемента разбивается на три линейных участка и для каждого из них  составляется линейное дифференциальное уравнение:

1 уч. 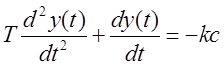 , если у>b

2 уч. 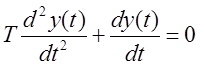 , если                                           

3 уч. 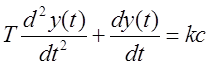 , если у<-b

Для фазовой плоскости введем координаты у и 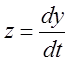. Исключим в уравнениях (1) время t.

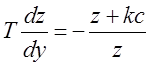
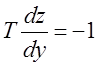
Для упрощения расчетов, приведем дифференциальные уравнения для каждого участка к системе двух дифференциальных уравнений первого порядка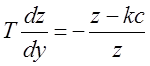

Получим уравнения фазовой траектории для участков 1-3 нелинейной характеристики:

1 уч. 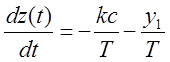 ,если у>b

2 уч. 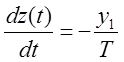 , если

3 уч. 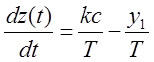 , если у<b

Для построения фазового портрета и переходного процесса нелинейной системы воспользуемся программой MathCad.

Зададим значения коэффициентов и начальные условия:

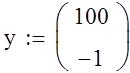
Определим функцию D по 3-м линейным участкам нелинейной статической характеристики, задающую производную, приведя дифференциальное уравнение 2-го порядка к системе 2-х дифференциальных уравнений 1-го порядка.

          Рисунок 12 - Фазовый портрет нелинейной системы регулирования

Построим переходный процесс, соответствующий данному фазовому портрету.

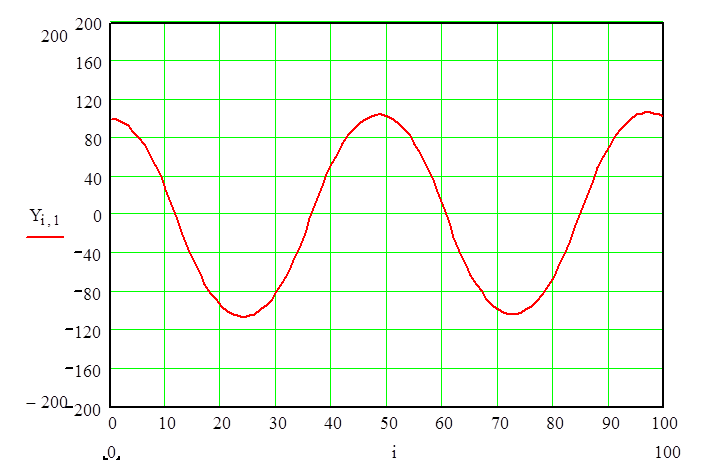
Рисунок 13 -   График переходного процесса нелинейной системы

Вывод: Из фазового портрета видно, что имеет место предельный цикл (устойчивость в большом), соответствующий незатухающим колебаниям в системе регулирования. Качество управления, о котором можно судить по виду фазового портрета является невысоким и требует дополнительной коррекции.

ЗАКЛЮЧЕНИЕ

   Целью курсовой работы являлось исследование и проведение анализа линейной и нелинейной системы автоматического регулирования.

В ходе выполнения курсовой работы был проведен расчет и анализ линейной системы автоматического регулирования давления пара перед турбиной энергоблока. Полученная линейная система имеет высокое качество регулирования, но и соответствующий уровень сложности. При заданных параметрах система устойчива с большим запасом устойчивости по амплитуде. Запас устойчивости по фазе бесконечен.

            При введении нелинейного элемента было предположено, что данная нелинейность упростит САР. После проведения расчетов и построения фазового портрета нелинейной системы можно сделать вывод, что введение нелинейности  привело к упрощению системы, а качество регулирования снизилось, т.к. имеет место предельный цикл (устойчивость в большом), соответствующий незатухающим колебаниям в системе.

          СПИСОК ЛИТЕРАТУРЫ

1. В.Н. Веллер Автоматическое регулирование паровых турбин. М: Наука 1987.

2. Г.П. Плетнев Автоматическое управление и защита теплоэнергетических установок электростанций М: Атомиздат 1989.

3. В.Я. Ротач, В.Ф. Кузищин Автоматические настройки систем управления С.-Пб.:1986

4. Ю. И. Топчеев Атлас для проектирования систем автоматического регулирования.

5. Д.В. Кирьянов Самоучитель MathCad 11. С.-Пб.: БХВм – Петербург, 2003. – 560 с.: ил.

6. Ю.Л. Кетков MATLAB 6.X: программирование численных методов. – С.-Пб.: БХВм – Петербург, 2004. – 672 с.: ил.

7. Н.Н. Иващенко Автоматическое регулирование М.: Машиностроение, 1978