Исследования системы регулирования энергоблока паровой котел – турбина, страница 2

          Структурная схема состоит из типовых звеньев, математическое описание которых задано в операторной форме. Связь между входом и выходом системы задается в виде передаточной функции W(p). В общем виде передаточную функцию можно представить в виде:

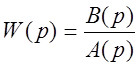
Под полюсами подразумеваются корни полинома – знаменателя А(р), а под нулями – корни полинома числителя В(р).

          Определим тип полученных звеньев функционально – структурной схеме.

Привод – интегрирующее звено (звено, в котором в установившемся режиме линейная зависимость связывает входную величину и производную выходную).

Данное звено имеет передаточную функцию вида:

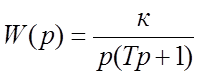
где к – коэффициент усиления звена;

      Т – задержка по времени.

Для привода определили:

к=5, Т=4,5, тогда

          Задвижка – инерционное звено 1-го порядка (звено, у которого при приложении какого-либо воздействия реакция возникает не сразу, а возрастает постепенно

Данное звено имеет передаточную функцию вида:

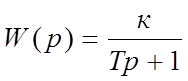
где к – коэффициент усиления звена;

      Т – задержка по времени.

Для задвижки определили:

к=1,2, Т=0,2, тогда

Топка котла - инерционное звено 1-го порядка.

Для топки котла определили:

к=0,1, Т=0,07, тогда

          Датчик давления (сильфон) – инерционное звено 1-го порядка.

Для датчика давления определили:

к=0,83, Т=0,12 тогда

          1.4 Составление и преобразование структурной схемы и расчет передаточной функции для замкнутой и разомкнутой систем

Структурная схема системы регулирования давления пара перед турбиной изображена на рисунке 3.

 

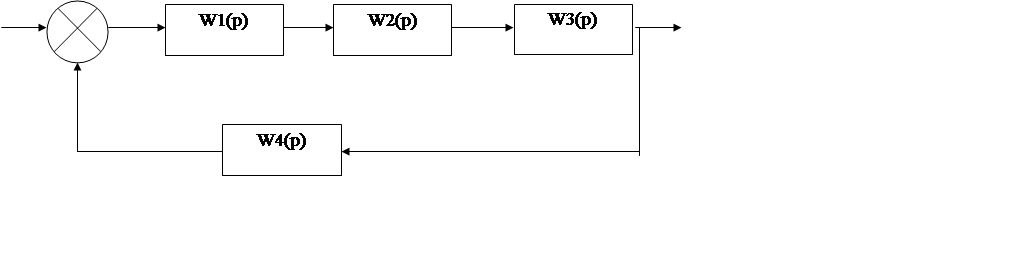
          Рисунок 3 - Структурная схема системы регулирования давления пара

Рассчитаем замкнутую систему.

Звенья соединенные последовательно могут быть заменены одним звеном с передаточной функцией W5(p) равной произведению последовательно соединенных звеньев W1(p), W2(p), W3(p).

Преобразованная структурная схема регулирования давления пара будет иметь вид (рисунок 4)

 

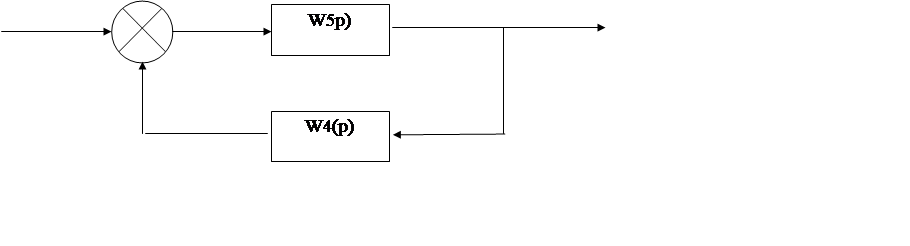          Рисунок 4 - Преобразованная структурная схема регулирования давления пара

          Оставшиеся два звена W5(p)  и W4(p) соединены встречно – параллельно. Значит общая передаточная функция замкнутой системы будет иметь вид:

 

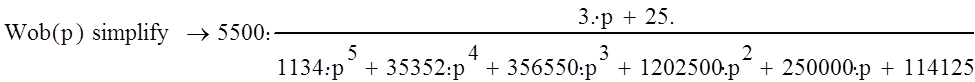          Рассчитаем разомкнутую систему.

Звенья разомкнутой системы соединенные последовательно и поэтому могут быть заменены одним звеном с передаточной функцией Wр(p) равной произведению последовательно соединенных звеньев W1(p), W2(p), W3(p), W4(p).

 

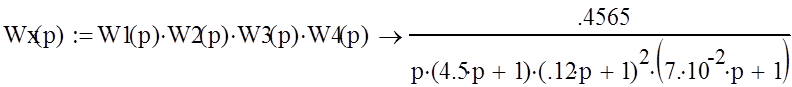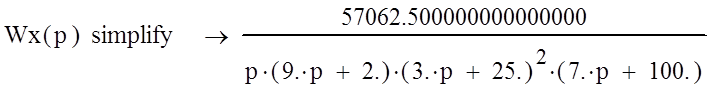          1.5 Определение устойчивости системы

Определим устойчивость системы по критерию Гурвица. Выпишем характеристическое уравнение системы:

          Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны. Определитель Гурвица составим по коэффициентам характеристического уравнения.

Все миноры определителя Гурвица положительны, следовательно, система устойчива.

          Определим устойчивость системы по критерию Найквиста. Расчет по критерию Найквиста производится для разомкнутой системы.

Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы корни полинома разомкнутой системы находились в левой части комплексной плоскости и годограф Найквиста не охватывал точку (-1;j0).

Передаточная функция замкнутой системы регулирования давления пара имеет вид:

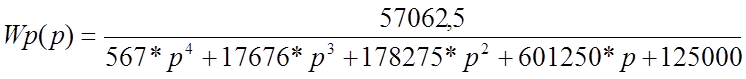
Возьмем полином разомкнутой системы и определим количество корней:

 

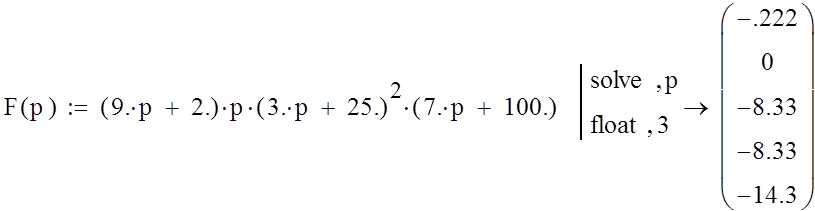Все корни полинома разомкнутой системы находятся в левой части комплексной плоскости.

Построим годограф Найквиста (рисунок 5) с помощью программы MathLab:

>> w=tf([57062.5],[567 17676 178275 601250 125000])

Transfer function:

                     5.706e004

----------------------------------------------------

567 s^4 + 17676 s^3 + 178275 s^2 + 601250 s + 125000

>> pole(w)

ans =

 -14.2857         

  -8.3333 + 0.0000i