Задачи автоматического управления. Линеаризация уравнений и звеньев систем автоматического управления

Лекция №5.

Статические характеристики исполнительных устройств, как правило, не линейные. Примеры:

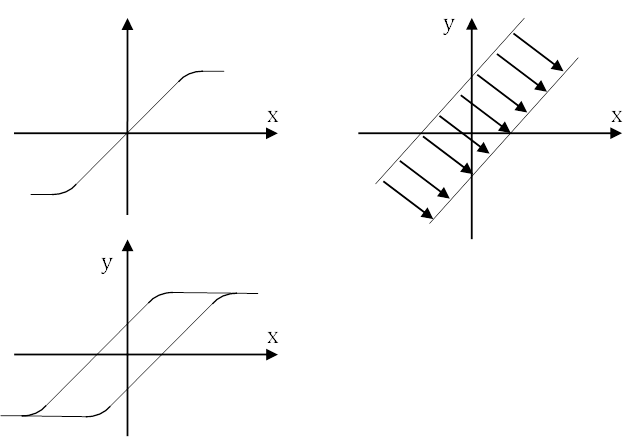Некоторые усилители мощности имеют гистерезисную статическую характеристику. Подобные характеристики могут принадлежать не только исполнительным устройствам, но и другим элементам системы управления.

Задачи автоматического управления.

Среди многообразия задач управления можно выразить 3 основных: задачи программного управления, стабилизации и слежения.

            Задачи программного управления.

В этих задачах используются полные математические модели объектов управления, которые могут задаваться уравнениями состояний.

 

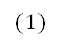
где  - вектор состояния объекта (капа?);  - вектор управляющих входов; F(t) – вектор возмущающих входов; Q(t) – вектор регулируемых выходов.

Пусть заданы начальные и конечные условия состояния объекта, которые выражают требования к качеству управления и отражают возможные ограничения на траекторию движения системы.

начальные условия:

конечные условия:

Задача программного управления заключается в нахождении такого управляющего воздействия μ(t), которое переводило бы объект из заданного начального состояния  в заданное конечное , так, чтобы выполнялись требуемые условия на управление и траекторию движения. В этом случае управление  будет называться программным управлением, а соответствующая ему траектория  будет называться программной траекторией.

В системе уравнений (1) отмечены внешние возмущения F(t). Как правило, возмущения изменяются непредсказуемо, поэтому в программном управлении определяют некоторое среднее или номинальное значение F(t). Причем очень часто это значение задают , тогда можно записать уравнение в другом виде:

 

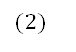
Система уравнений (2) будет называться системой невозмущенного движения, соответственно решение системы уравнений (2) будет также называться системой невозмущенного движения.

            Задачи слежения.

При описании объекта управления используют полную математическую модель объекта уравнения (1). Суть задачи состоит в следующем: требуется определить уравнение и параметры регулятора, работающего по принципу обратной связи, так чтобы выходные переменные Q(t) отслеживали задающее воздействие q(t).

Главным требованием в задаче слежения является требование устойчивости системы.

 (3)

Другими требованиями могут быть – точность слежения, быстродействие, грубость и так далее.

Основным отличаем от задач стабилизации и задач программного управления является то, что задающие воздействия q(t) заранее неизвестны, и могут меняться непредвиденным образом, часто это случайные вектор-функции о которых известно лишь их поведение в статическом смысле (в конкретный момент времени). Поэтому, невозможно сформировать программное управление чтобы обеспечить движение объекта по заданной траектории. При рассмотрении задач слежения используют полные уравнения объекта.

            Задачи стабилизации.

Точно реализовать требуемое движение каппа от т и Q(t) практически невозможно. Причинами являются – неточное задание начальных условий, неточная реализация программных управлений, влияние внешних возмущений, отличных от нуля. В результате истинное движение объекта будет отличаться от программного, такие задачи решают задачи стабилизации. Для описания объекта в этом случае используют уравнения, описывающие отклонения истинного движения от программного. Эти уравнения называются уравнениями возмущенного движения.

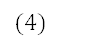
 - векторы отклонения действительного движения от заданного значения (*) – действительное остальное заданное движение;  – вектор отклонения воздействия;

 - начальное отклонение переменных состояния объекта;  - изменение внешних возмущений.

В задачах программного управления требуемое управление является функцией времени. В задачах же стабилизации требуется определить добавки в программном управлении так, чтобы заставить объект под действием полного управления двигаться по программной траектории или вблизи от нее.

Поскольку, начальные отклонения и изменения внешних возмущений обычно неизвестны, то управление ищется не как функция времени, а как функция изменяемых переменных (данные с датчиков), которые содержат информацию об отклонении. То есть, в задачах стабилизации требуется определить уравнения и параметры регулятора, работающего по принципу обратной связи.

Основным требованием является условие:                                                               – это условие асимптотической устойчивости системы.

            Линеаризация уравнений и звеньев систем автоматического управления.

Линеаризация заключается в переходе к линейному дифференциальному равнению, переменные которого являются отклонениями от некоторого номинального режима.  и  (примем возмущение f = 0), описывают траекторию движения системы, если запишем уравнение движения системы:

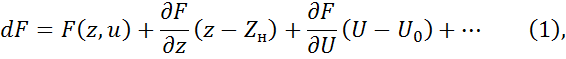
так как уравнение с частными производными это нелинейное уравнение, т.е. частный случай решения.

Отбросим малые члены уравнения (1):

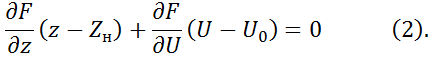
Уравнение (2) является приближенно линеаризованным уравнением, в этом уравнении  и  являются коэффициентами ряда Тейлора.

Введем новые переменные: отклонение от номинального

 

Так как все частные производные представляют из себя либо постоянные матрицы, либо матрицы, зависящие только от времени, то уравнение (2) с учетом допущений (3) есть либо система линейных дифференциальных уравнений с постоянными коэффициентами, относительно отклонений (3), либо система с переменными коэффициентами. Постоянство или переменность коэффициентов зависит от номинальной траектории. Например, в системах стабилизации, где номинальные траектории константы, получают постоянные матрицы. Таким образом, переходя к уравнениям в отклонениях, получаем системы линейных дифференциальных уравнений, которую будем рассматривать относительно выходной величины. Порядок этой системы равен порядку производной по y. Дифференцирование же входного сигнала рассматривается не как дифференциальное уравнение относительно сигнала u, а как операция с известным входным сигналом. То есть получаем дифференциальное уравнение вида:

A₀(t), A₁(t), … ,A_n(t) и B₀(t), B₁(t), … , B_n(t) – матрицы, которые описывают номинальную траекторию движения системы.

При удачной номинальной траектории матрицы А и В становятся постоянными, и для такой системы дифференциальных уравнений с постоянными коэффициентами можно получить до конца точное решение и полностью его исследовать. В случае постоянных коэффициентов система называется стационарной. Чаще всего входные и выходные величины это скалярные функции, то есть в системе имеется лишь по одному входу и одному выходу (одномерные системы), тогда матрицы превращаются в числа. Перепишем уравнение:

Переход от дифференциального уравнения n-ного порядка к системе из n-дифференциальных уравнений 1-го порядка.