


Анализ свойств НЕЛИНЕЙНЫХ сау с разнотемповыми движениями
Нелинейные системы описываются нелинейными дифференциальными уравнениями общих методов решения, которых нет. Анализ систем выполняется обходимыми приемами, одним из которых является метод фазового пространства.
Фаза или
состояние системы характеризуется рядом параметров: входной ![]() и выходной
и выходной ![]() величиной,
скоростного изменения выходной величины
величиной,
скоростного изменения выходной величины ![]() ,
точностью управления
,
точностью управления ![]() и т.д. Чем выше порядок системы,
тем больше параметров, описывающих состояние системы. Для системы n-го порядка
параметров, характеризующих состояние системы должно быть
и т.д. Чем выше порядок системы,
тем больше параметров, описывающих состояние системы. Для системы n-го порядка
параметров, характеризующих состояние системы должно быть ![]() .
.
Набору координат соответствует n-мерное пространство с одноименными координатами осей. Это пространство называется фазовым. Если состояние системы меняется, то соответствующая точка начинает перемещаться в фазовом пространстве, вычерчивая кривую, называемую фазовой траекторией. Фазовая траектория является исчерпывающей характеристикой поведения системы.
В реальных системах наличие звеньев с малыми инерционностями может приводить к возникновению разнотемповых процессов, для выделения которых используют метод разделения движений. При этом уравнения исследуемой системы должны быть представлены в стандартной форме:
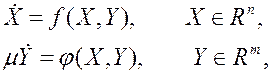 (1)
(1)
где функции ![]() и
и ![]() соизмеримы по норме в рабочей области
пространства состояний.
соизмеримы по норме в рабочей области
пространства состояний.
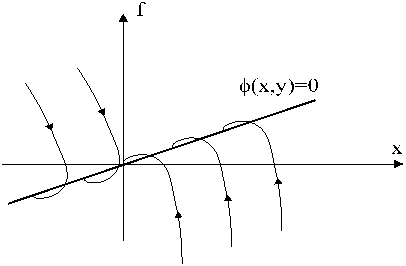
Рисунок 1 – Траектории движения разнотемповых систем
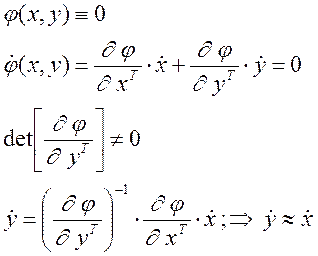
Для систем типа (*) можно выделить две фазы движения:
1- движение из произвольных н.у. к поверхности.
2- движение вдоль поверхности.
Такие системы называют также системами с разнотемповыми процессами.
Свойства систем с разнотемповым движением:
1) При движении из начальных условий, не
лежащих на поверхности ![]() , скорость изменения
переменной
, скорость изменения
переменной ![]() на порядок выше, чем
на порядок выше, чем ![]() .
.
2) Если начальные условия находятся на
поверхности ![]() , то скорости изменения переменных
, то скорости изменения переменных ![]() и
и ![]() будут
соизмеримы.
будут
соизмеримы.
В асимптотике поведение медленной составляющей движения описывается уравнениями:
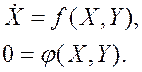
Если теперь
определить ![]() , то подставив его в уравнение для X, получим
подсистему медленных движений в виде:
, то подставив его в уравнение для X, получим
подсистему медленных движений в виде:
![]() (2)
(2)
Поведение быстрой составляющей движения соответствует уравнению:
![]() (3)
(3)
Как видно,
системы (2) и (3) независимы, а степень разделения движений определяется
численным значением ![]() .
.
Для линейных систем критерием разделимости движений может служить распределение корней на комплексной плоскости (рисунок 1). Формальной оценкой степени разделимости является величина:
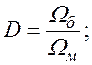 (4)
(4)
где ![]() и
и ![]() - обобщенный корень соответственно
подсистемы быстрых и медленных движений. Принято считать, что разделение
движений справедливо с достаточной точностью, если
- обобщенный корень соответственно
подсистемы быстрых и медленных движений. Принято считать, что разделение
движений справедливо с достаточной точностью, если ![]() .
.
Корни, расположенные вблизи начала координат, определяют медленную составляющую движений. Процессы, соответствующие далеким корням, протекают быстро.
В случае нелинейных систем можно анализировать корни линеаризованных подсистем быстрых и медленных движений. Однако эта процедура справедлива лишь в малой окрестности точки линеаризации. По этой причине основным условием применения метода разделения движений является физическое наличие в системе малых инерционностей или больших коэффициентов.
 |
1.
Приступая
к работе, необходимо предварительно выделить быструю и медленную составляющие
движений в исходной системе для двух типов звеньев с малой инерционностью ![]() и определить значение
и определить значение ![]() , при котором такое разделение движений
справедливо.
, при котором такое разделение движений
справедливо.
2. При исследовании свойств системы с помощью пакета прикладных программ следует в качестве метода интегрирования использовать метод Рунге-Кутта 4 порядка, причем шаг интегрирования уменьшить в 2 раза.
1.Подготовить модель системы, структурная схема которой приведена на рисунок 2.
Оценить качество переходного процесса по
переменным ![]() ,
, ![]() и
и ![]() при V=1 и M(t)=0. Получить
проекцию фазового портрета системы на плоскость
при V=1 и M(t)=0. Получить
проекцию фазового портрета системы на плоскость ![]() .
.
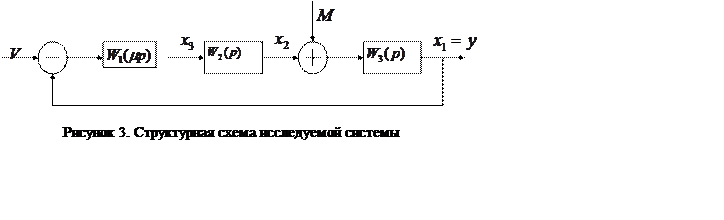
Здесь:
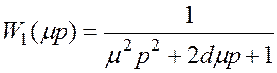 ;
; 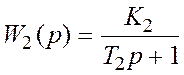 ;
; 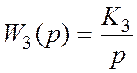 .
.
Параметры передаточных функций приведены в таблице 1.
Таблица 1.
|
Параметр |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
K2 |
2 |
5 |
1 |
3 |
2 |
4 |
6 |
8 |
|
T2 |
0,5 |
0,3 |
0,6 |
0,8 |
0,4 |
0,3 |
0,5 |
0,4 |
|
d |
0,8 |
0,5 |
0,7 |
0,5 |
0,6 |
0,8 |
0,6 |
0,7 |
|
K3 |
3 |
1 |
4 |
2 |
5 |
1 |
2 |
1 |
|
m |
0,3 |
0,4 |
0,5 |
0,3 |
0,2 |
0,5 |
0,1 |
0,2 |
2.Уменьшая
последовательно m в 5, 10 и 40
раз, зарисовать переходные процессы ![]() ,
, ![]() и
и ![]() (все
графики представить на одном рисунке) и проекцию фазового портрета системы
(также на одном рисунке). По данным эксперимента определить возможность
разделения движений.
(все
графики представить на одном рисунке) и проекцию фазового портрета системы
(также на одном рисунке). По данным эксперимента определить возможность
разделения движений.
3.Оценить качество
переходного процесса (tп и s%) для переменных
![]() и
и ![]() при
рассчитанном значении
при
рассчитанном значении ![]() . Анализируя процесс
. Анализируя процесс ![]() , время моделирования нужно задавать не
более 0.5 с.
, время моделирования нужно задавать не
более 0.5 с.
4.При ![]() исследовать влияние d, выбирая его
значение в диапазоне (0,1-1), на фазовый портрет и переходные процессы
исследовать влияние d, выбирая его
значение в диапазоне (0,1-1), на фазовый портрет и переходные процессы ![]() и
и ![]() (графики
представлять на одном рисунке).
(графики
представлять на одном рисунке).
5.Исследовать влияние T2 на фазовый портрет системы, а также медленную и быструю составляющие движения. С этой целью необходимо сначала увеличить, а затем уменьшить в 3 раза T2 относительно номинального значения.
6.При том же
значении ![]() оценить влияние K2на переходные
процессы и фазовый портрет системы, последовательно увеличивая и уменьшая
коэффициент в 2 раза относительно K2ном.
оценить влияние K2на переходные
процессы и фазовый портрет системы, последовательно увеличивая и уменьшая
коэффициент в 2 раза относительно K2ном.
7.Зарисовать
проекцию фазового портрета и переходные процессы для переменных ![]() ,
, ![]() и
и ![]() при
при ![]() , V=0 и M(t-t)=1, здесь t=1с - время
возникновения возмущающего воздействия.
, V=0 и M(t-t)=1, здесь t=1с - время
возникновения возмущающего воздействия.
8.В исходной системе разделить движения и исследовать порознь быструю и медленную составляющие. Оценить для каждой из них tп и s% и сравнить с результатами п. 3.
9.Заменить колебательное звено на входе системы (рисунок 2.) апериодическим с передаточной функцией:
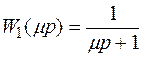
10. Повторить п. 3. и п. 8. Сравнить полученные результаты с аналогичными для исходной системы.
1. Цель работы.
2. Структурные схемы исследованных систем.
3. Уравнения ПМД и
ПБД, рассчитанное значение ![]() .
.
4. Графики всех переходных процессов и фазовые портреты.
5. Экспериментально найденные значения tп и s% для пп. 3, 8 и 9.
6. Выводы по работе.
1. Как влияют параметры быстрой подсистемы на качество процессов в исходной системе?
2. При каких условиях можно пренебречь малыми инерционностями?
3. Как влияют параметры подсистемы медленных движений на процессы в исходной системы?
4. Как оценить возможность разделения движений в системе?
5. Существует ли взаимосвязь между устойчивостью ПМД, ПБД и исходной системой?
6. С какой целью разделяют движения в системе?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.