




Практичне заняття №1.
“Табличне інтегрування. Обчислення інтегралів
(метод заміни перемінного, метод інтегрування вроздріб)”
I. Табличне інтегрування. Таблиця основних інтегралів
1) 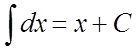 . 2)
. 2) 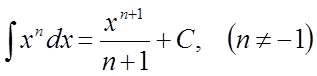 .
.
3) 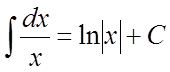 . 4)
. 4) 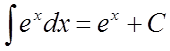 .
.
5) 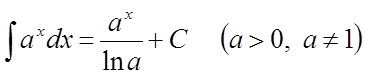 . 6)
. 6) 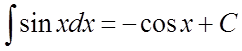 .
.
7) 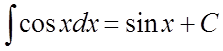 . 8)
. 8) 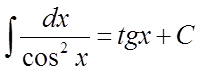 .
.
9) 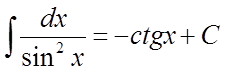 . 10)
. 10) 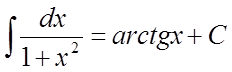 .
.
11) 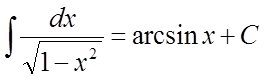 . 12)
. 12) 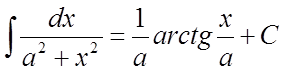 .
.
13) 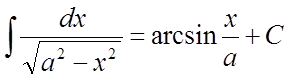 . 14)
. 14) 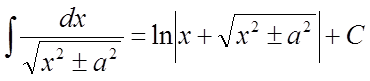 .
.
15) 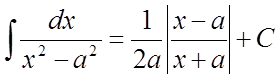 .
.
Приклад 1.
Використовуючи табличні інтеграли, знайти
інтеграл 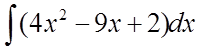 .
.
Рішення.
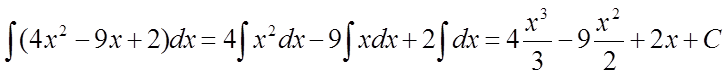 .
.
Використовували властивості інтегралів 4 і 5, а також формули 1, 2.
Приклад 2.
Використовуючи табличні інтеграли, знайти
інтеграл 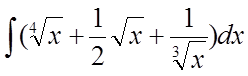 .
.
Рішення.
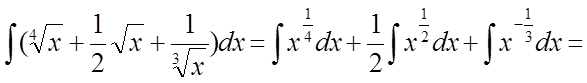
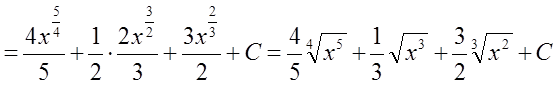 .
.
Приклад 3.
Використовуючи табличні інтеграли, знайти
інтеграл 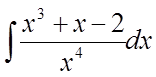 .
.
Рішення.
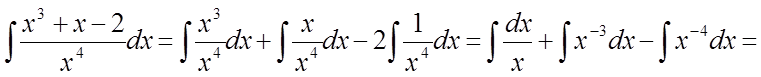
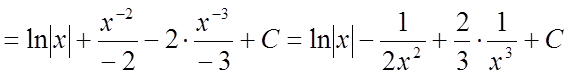 .
.
Приклад 4.
Використовуючи табличні інтеграли, знайти
інтеграл 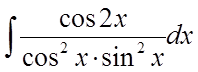 .
.
Рішення.
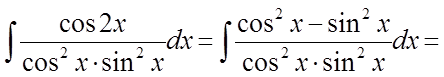
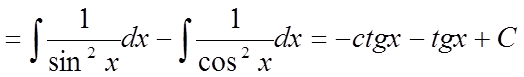 .
.
Перетворимо
підінтегральну функцію, використовувавши формулу ![]() , і
розділимо почленно чисельник і знаменник.
, і
розділимо почленно чисельник і знаменник.
II. Метод підстановки або заміни перемінної
Якщо
підінтегральна функція має вигляд ![]() , то заміняють
, то заміняють ![]() і в такий спосіб від складної функції
переходять до простій
і в такий спосіб від складної функції
переходять до простій ![]() . Увівши позначення
. Увівши позначення ![]() і продиференціювавши обидві частини цієї
рівності:
і продиференціювавши обидві частини цієї
рівності: ![]() , тобто інтеграл приводиться до табличного,
після узяття інтеграла, тобто визначення первісної функції
, тобто інтеграл приводиться до табличного,
після узяття інтеграла, тобто визначення первісної функції ![]() , повертаються до перемінного х.
, повертаються до перемінного х.
Приклад 1.
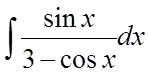 .
.Рішення.
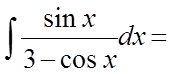

Приклад 2.
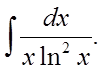 .
.Рішення.
Тому що 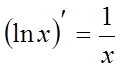 , позначимо
, позначимо ![]() , тоді
, тоді 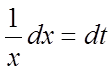 і
і
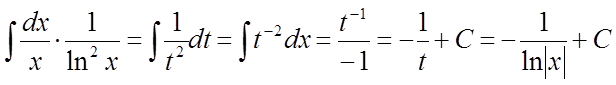 .
.
Приклад 3.
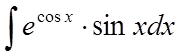 .
.Рішення.
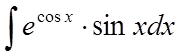 .
.
Помітивши, що
похідна ![]() дорівнює
дорівнює ![]() ,
замінимо:
,
замінимо:
![]() ,
, ![]() ,
,
і тоді 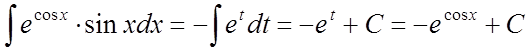 .
.
Приклад 4.
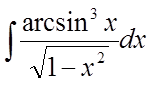 .
.Рішення
Тому що 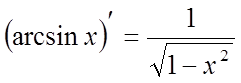 , то робимо заміну
, то робимо заміну ![]() і
і
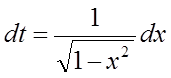 .
.
Отже, 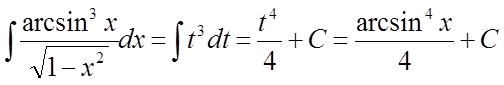 .
.
III. Метод інтегрування вроздріб
Нехай ![]() і
і ![]() –
безперервні, диференціюємі функції. Відомо, що
–
безперервні, диференціюємі функції. Відомо, що 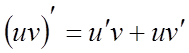 .
.
Проінтегруємо обидві частини цієї рівності:
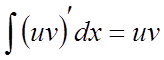 ,
, ![]() і
і ![]() і
і ![]() , отже
, отже 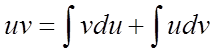 , або остаточно
, або остаточно
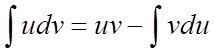 – формула інтегрування вроздріб.
– формула інтегрування вроздріб.
Приклад 1.
Методом
інтегрування вроздріб знайти 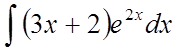 .
.
Рішення.
Позначимо 3х+2=u
і диференціюємо: ![]() ,
, ![]()
інтегруємо: 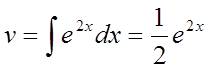 .
.
Підставивши у формулу інтегрування вроздріб, одержимо:
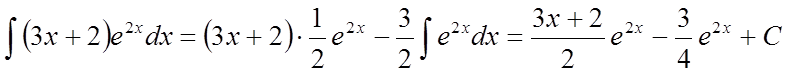 .
.
Приклад 2.
Методом
інтегрування вроздріб знайти 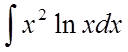 .
.
Рішення.
Позначимо ![]() ,
, 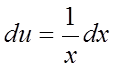 ,
, ![]() ,
, 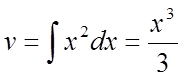 .
.
Маємо 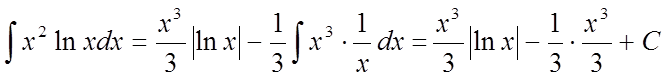 .
.
Приклад 3.
Методом
інтегрування вроздріб знайти 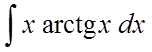 .
.
Рішення.
Позначимо ![]() ,
, 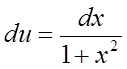 ,
, ![]() ,
, 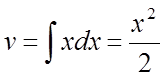 .
.
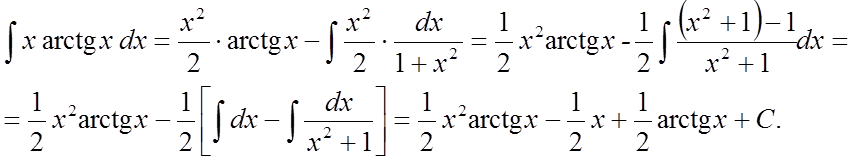
Приклад 4.
Методом
інтегрування вроздріб знайти 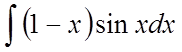 .
.
Рішення.
Позначимо ![]() ,
, ![]() ,
, ![]() ,
, 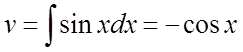 .
.
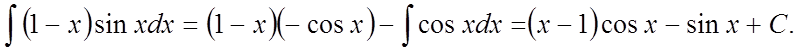 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.