Пособие к курсовому проектированию по антенно-фидерным устройствам, страница 4

Здесь I_m – комплексная амплитуда тока в пучности m–го вибратора антенны с рефлектором.

Решения системы уравнений (1.6) определяются через решения системы уравнений (1.1), т.е. через токи антенны без рефлектора, следующим образом:

                                              (1.7)

При этом система уравнения (1.6) переходит в следующую:

                                           (1.8)

Коэффициенты W_m определяются методом последовательного решения. Сначала рассчитываются W_m для наименьшего и наибольшего значения m (m=0 и m=N), а затем по найденным их значениям последовательно рассчитываются значения W_m равноудаленные от крайних. Соответственно эти коэффициенты определяются следующими соотношениями:

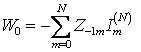;                                                                           (1.9)

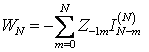                                                                        (1.10)

и для случая 0<υ<N (для неизвестных, равноудаленных от крайних W₀ и W_N, например, при N=4, W₁ и W₃ и затем W₂) формулами

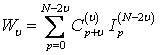;                                                                    (1.11)

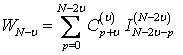,                                                                (1.12)

где

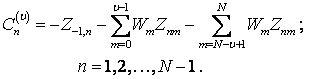                                       (1.13)

Например, для υ=1

.

Как следует из формул (1.8) и (1.9), ток в рефлекторе

.                                                                  (1.14)

1.3. РАСЧЕТ СОПРОТИВЛЕНИЙ АНТЕННЫ

1.3.1. Расчет собственных сопротивлений вибраторов

Для вибраторов, длина 2l которых близка  к λ/2, можно допустить, что собственное  сопротивление  определяется формулой

.                                                          (1.15)

Для прямолинейного тонкого вибратора с круглым поперечным сечением и  длиной, близкой к λ/2, реактивная часть сопротивления

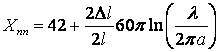 Ом.                                                  (1.16)

Здесь а – радиус  поперечного сечения  вибратора;

 (укорочение или удлинение вибратора по сравнению с λ/2).

В приведенной формуле не имеет смысла учитывать поправки строгой теории, основанной на решении задачи о поле вибратора как эллипсоида  вращения, так как весь метод расчета антенны основан на методе наведенных ЭДС, использованном при  получении формулы (1.16).

1.3.2. Расчет наведенных сопротивлений

Взаимное сопротивление вибраторов Z_nm антенны определяется по таблицам для полуволновых вибраторов.

1.3.3. Расчет входного сопротивления антенны

Входное сопротивление антенны (активного вибратора, возбуждающего антенну), отнесенное к пучности тока, определяется следующими формулами:

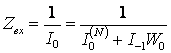 ;                                                                  (1.17)

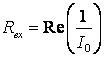 ;                                                                               (1.18)