Пособие к курсовому проектированию по антенно-фидерным устройствам, страница 3

Система уравнений, определяющих токи в вибраторах антенны без рефлектора, имеет вид

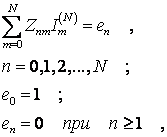                                                                      (1.1)

где  – комплексная амплитуда тока в пучности m–го вибратора для антенны, имеющей N пассивных директоров.

Например, для антенны из трех вибраторов (активный и два директора, N =2) система уравнений

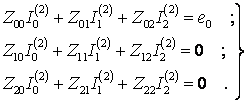
Для упрощения решения системы (1.1)  удобно принять e₀=1B, так как форма диаграммы направленности зависит не от величины токов в элементах антенны, а от соотношения между ними. Способ решения системы (1.1) может быть любым. При большом количестве директоров наиболее удобен способ последовательного решения, при котором сначала определяются токи в антенне, состоящей из одного активного вибратора; затем с помощью найденного решения определяются токи в антенне, состоящей из активного вибратора и одного директора, далее по этим токам определяются токи в антенне с двумя директорами и т.д. Расчет ведется с помощью рекуррентной формулы Леонтовича, которая позволяет найти решение системы уравнений для антенны, имеющей N+1 пассивных директоров:

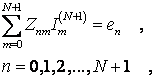                                                                         (1.2)

если известно решение системы (1.1) для антенны с N директорами, т.е. если известны токи . При этом собственные реактивные сопротивления всех вибраторов принимаются одинаковыми:

X₀₀=X₁₁=X₂₂=… .

Рекуррентная формула для  тока в m–м вибраторе антенны с N+1 директорами имеет следующий вид:

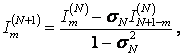                                                                   (1.3)

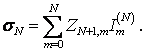где                                                                               (1.4)

При развертывании формулы (1.3) появляется слагаемое , которое представляет собой ток в отсутствующем вибраторе, по физическому смыслу равный нулю:

                                                                                         (1.5)

Правило пользования формулами (1.3), (1.4) и (1.5) заключается в следующем. Предположим, что антенна состоит только из одного активного вибратора (N=0). Амплитуда тока в нем

так как  e_o=1.

Для определения токов в антенне из одного активного вибратора и одного пассивного директора (N+1=1) воспользуемся формулами (1.3), (1.4), (1.5). По формуле (1.4) находим

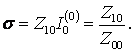
Затем для определения токов используем формулу (1.3) с учетом формулы (1.5). Ток в активном вибраторе определится формулой

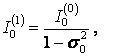так как  

Ток в директоре

.

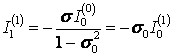Далее увеличиваем на единицу число директоров и указанным способом с помощью формул (1.3), (1.4), (1.5) определяем последовательно токи во всех вибраторах антенны.

1.2.2. Решение задачи для антенны с рефлектором

Для антенны с рефлектором система уравнений, определяющих токи в вибраторах, может быть записана следующим образом:

для всех вибраторов, кроме рефлектора,

и для рефлектора            (1.6)