


Лекція 3
План.
1. Знакоперемінні ряди. Ряди, що знакочергуються.
2. Теорема Лейбніца.
3. Оцінка залишку. Абсолютна й умовна збіжність рядів.
1. Знакоперемінні ряди. Ряди, що знакочергуються
Визначення 1. Ряд називається знакочергуючимся, якщо будь-які його члени, що стоять поруч мають протилежні знаки
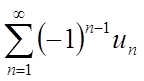 . (1)
. (1)
Тут ![]() – позитивні.
– позитивні.
Визначення 2. Ряд називається знакоперемінним, якщо серед його членів маються як позитивні, так і негативні (знакочергуючийся ряд – окремий випадок знакоперемінного).
2. Теорема
Лейбница.
Якщо в знакочергуючомуся ряді 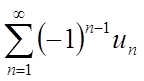 (1)
(1) ![]() члени такі, що
члени такі, що
1. ![]()
2. 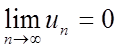 ,
,
то ряд (1) збігається, його сума позитивна і не перевершує першого члена ряду.
Доказ.
Розглянемо суму ![]() перших членів ряду (1)
перших членів ряду (1)
![]() .
.
З умови (1) випливає, що ![]() .
.
Перепишемо цю суму інакше
![]() .
.
Кожна дужка позитивна в силу умови
(1). Тому ![]() . Таким чином,
. Таким чином, ![]() при
зростанні m зростає й обмежена зверху. Звідси випливає, що
при
зростанні m зростає й обмежена зверху. Звідси випливає, що ![]() має межу S.
має межу S.
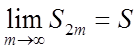 ,
, ![]() .
.
Доведена лише збіжність парних сум. Розглянемо непарну суму
![]() .
.
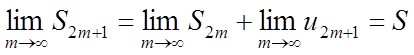 – у
силу умови (2) теореми.
– у
силу умови (2) теореми.
Тобто ряд (1) збігається.
Наприклад: 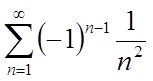
1) 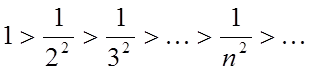
2) 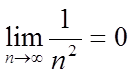 .
.
Отже, по теоремі Лейбніца ряд збігається.
(оцінка залишку знакочергуючогося ряду)
Якщо
знакочергуючийся ряд задовольняє умові теореми Лейбніца, то можна оцінити
помилку, що вийде, якщо замінити його суму S частковою сумою ![]() . При такій заміні відкидаються всі члени
ряду починаючи с.
. При такій заміні відкидаються всі члени
ряду починаючи с.![]() Але ці числа самі утворять
знакочергуючийся ряд, сума якого по абсолютній величині менше першого члена
цього ряду, тобто
Але ці числа самі утворять
знакочергуючийся ряд, сума якого по абсолютній величині менше першого члена
цього ряду, тобто ![]() . Виходить, помилка, зроблена при
заміні S на
. Виходить, помилка, зроблена при
заміні S на ![]() , не перевершує по абсолютній
величині перших з відкинутих членів.
, не перевершує по абсолютній
величині перших з відкинутих членів.
Визначення. Знакоперемінний ряд називається абсолютно збігаючимся, якщо збігається ряд, складений з абсолютних величин його членів.
Наприклад: 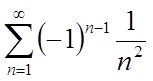 – ряд збігається по ознаці Лейбніца.
– ряд збігається по ознаці Лейбніца.
Складемо ряд з
абсолютних величин його членів. 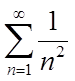 – збігається, це
випливає з інтегральної ознаки Коші. Тоді по визначенню сам знакоперемінний ряд
– збігається, це
випливає з інтегральної ознаки Коші. Тоді по визначенню сам знакоперемінний ряд
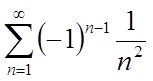 збігається абсолютно.
збігається абсолютно.
Визначення. Знакоперемінний ряд називається умовно збігаючимся, якщо він збігається, а ряд, складений з абсолютних величин членів знакоперемінного ряду, розбігається.
Наприклад: 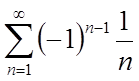
Знакочергуючийся
ряд збігається по ознаці Лейбніца. Ряд, складений з абсолютних величин членів 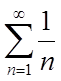 – розбігається. Це випливає з інтегральної
ознаки Коші. Виходить, знакочергуючийся ряд умовно збігається.
– розбігається. Це випливає з інтегральної
ознаки Коші. Виходить, знакочергуючийся ряд умовно збігається.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.