Розв’язання. Спочатку з’ясуємо
якими поверхнями обмежене задане тіло . Для цього зведемо рівняння поверхонь до
канонічної форми , перейшовши від нерівностей до рівностей. ![]() це сфера з центром в.т О(0;0;0) і
радіусом 8, а
це сфера з центром в.т О(0;0;0) і
радіусом 8, а ![]() - це весь трьохвимірний
простір за вийнятком внутрішніх точок (точок, які лежать всередині сфери) .
- це весь трьохвимірний
простір за вийнятком внутрішніх точок (точок, які лежать всередині сфери) .
Анолггічно ![]() це сфера з центром
в.т О(0;0;0) і радіусом 14, а
це сфера з центром
в.т О(0;0;0) і радіусом 14, а ![]() - це множина точок,
які лежать в середині сфери і на ній. Таким чином нерівність
- це множина точок,
які лежать в середині сфери і на ній. Таким чином нерівність![]() задає сферичне тіло радіусом 14 з вирізаною всередині
його сферою радіусом 8.
задає сферичне тіло радіусом 14 з вирізаною всередині
його сферою радіусом 8.
Нерівність 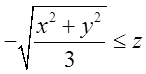 перетворимо
в рівність
перетворимо
в рівність 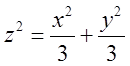 і побачимо, що це конус, а тому нерівність
і побачимо, що це конус, а тому нерівність
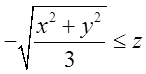 задає множину точок, яка лежить више
конуса
задає множину точок, яка лежить више
конуса 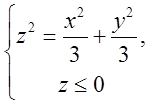 Анологічно
Анологічно
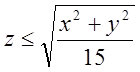 , множина точок , які лежать зовні нижче
конуса
, множина точок , які лежать зовні нижче
конуса 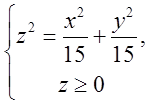
![]() – площина,
– площина, ![]() –
площина . Нерівність
–
площина . Нерівність
![]() – множина точок, які лежать між цими двома
площинами .
– множина точок, які лежать між цими двома
площинами .
Наявність виразів х2+у2+z2 спорукає нас на перехід до сферичної системи координат:
![]() . Переведемо рівняння
границь в нову систему координат.
. Переведемо рівняння
границь в нову систему координат.
1. ![]()
![]() . Це і є границі інтегрування по
. Це і є границі інтегрування по![]() .
.
2. 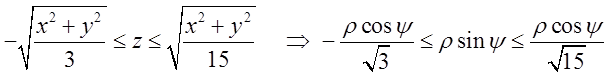
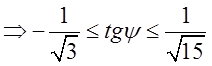 . Звідси легко знайти границі інтегрування по
. Звідси легко знайти границі інтегрування по ![]() :
: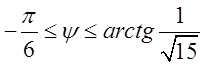 .
.
3.
![]()
![]()
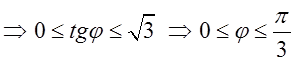 . Це і будуть границі інтегрування по
. Це і будуть границі інтегрування по ![]() .
.
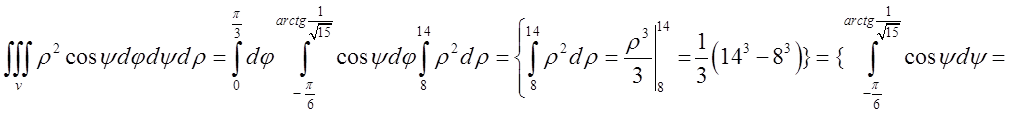
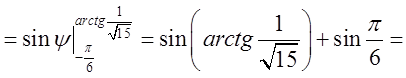
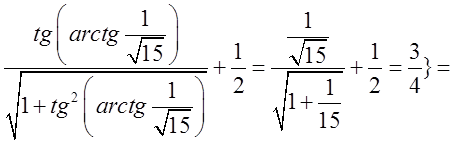
=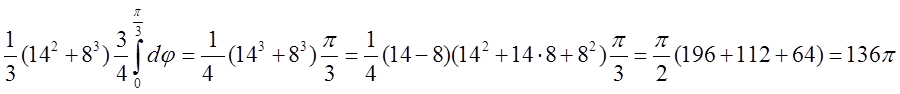
Відповідь. V=![]() куб. одиниць.
куб. одиниць.
П.6. Знайти масу тіла обмеженого поверхнями
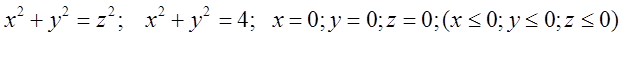 з густиною
з густиною 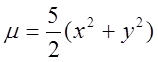 .
.
Розв’язок.
Тіло є четверта частина циліндра, з вирізним конусом
наявність виразу х2+у2 спонукає нас на перехід від
прямокутної декартової до циліндричної системи координат. ![]()
Проекция тіла на площинуХОY буде
чверть круга АОВ, а тому 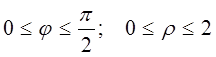 .
Нижня границя інтегрування по h знаходиться з умови, що
.
Нижня границя інтегрування по h знаходиться з умови, що ![]() , щоб знайти верхню границю інтегрування по
h, підставимо формули переходу в рівняння конуса,
тобто запишемо його в циліндричній системі координат:
, щоб знайти верхню границю інтегрування по
h, підставимо формули переходу в рівняння конуса,
тобто запишемо його в циліндричній системі координат:
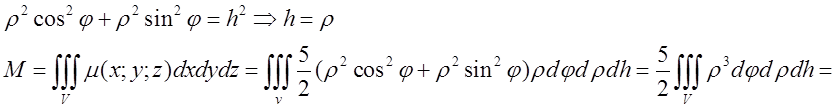
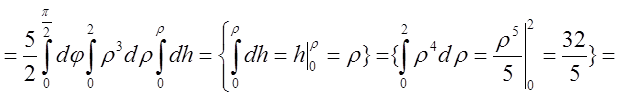
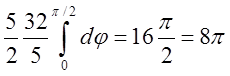 .
.
Відповідь. ![]() (одиниць маси).
(одиниць маси).
П.7. Обчислити поверхню тіла, яке утвориться приперетині двох циліндрів однакового радіуса R так, що їх вісі співпадають з осями координат.
Розв’язок. Фігура схожа на октаедр
(дві чотирикутні піраміди приставлені основами одна до одної), але всі вісім її
бокових граней зігнуті в циліндричну поверхню. Проекція поверхні фігури на
площину хОу буде квадрат зі стороною 2R і початком координат в точці перетину його діагоналей,
які є проекціями бічних ребер фігури. Діагоналі разом з вісями координат
розбили D на вісім прямокутних
трикутники. Візьмемо один з них, а саме той, який обмежений прямими ![]() . На нього проектується вернхня і
нижня частина поверхні фігури, з рівнінням
. На нього проектується вернхня і
нижня частина поверхні фігури, з рівнінням ![]() . І так
на кожен з восьми трикутників проектується верхня й нижня частина поверхні.
Тому
. І так
на кожен з восьми трикутників проектується верхня й нижня частина поверхні.
Тому ![]() , де
, де ![]() - площа
АDB (половина одної із
вісьми граней).
- площа
АDB (половина одної із
вісьми граней). 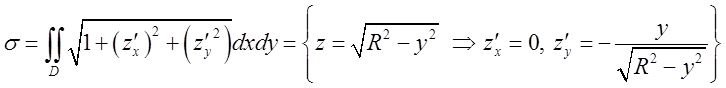 =
=
=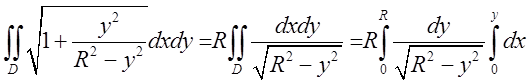 =
=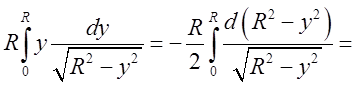
=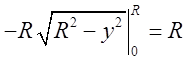 . Вся
площа поверхні буде дорівнювати 16R (кв. одиниць довж.)
. Вся
площа поверхні буде дорівнювати 16R (кв. одиниць довж.)
Запитання для самоперевірки.
1. Чому дорівнює площа плоскої фігури розташованої на площині хОу?
2.
Чому
дорівнює площа поверхні фігури ![]() з проекцією D на площину хОу?
з проекцією D на площину хОу?
3.
Чому
дорівнює об’єм циліндричної фігури обмеженої зверху ![]() знизу
знизу ![]() ?
?
4.
Чому
дорівнює маса плоскої фігури D розташованої на площині хОу, поверхнева густина якої ![]() ?
?
5.
Чому
дорівнює маса об’ємної фігури V густина якої ![]() ?
?
6.
Чому
дорівнюють статичні моменти плоскої фігури D розташованої на
площині хОу, поверхнева густина якої ![]() ?
?
7.
Чому
дорівнюють статичні моменти відносно координатних площин об’ємної фігури V, густина якої ![]() ?
?
8.
Чому
дорівнюють координати![]() центра ваги плоскої фігури D розташованої на
площині хОу, поверхнева густина якої
центра ваги плоскої фігури D розташованої на
площині хОу, поверхнева густина якої ![]() ?
?
9.
Чому
дорівнюють координати![]() центра ваги неоднорідної об’ємної фігури V, густина якої
центра ваги неоднорідної об’ємної фігури V, густина якої ![]() ?
?
10. Чому дорівнюють моменти
інерції відносно осей координат плоскої фігури D розташованої на площині хОу, з
поверхневою густиною ![]() ?
?
11. Чому дорівнюють моменти
інерції відносно осей неоднорідної об’ємної фігури V, густина якої ![]() ?
?
12. Чому дорівнює
відцентровий момент інерції плоскої пластинки, густина якої ![]() ?
?
13. Чому дорівнює полярний
момент інерції плоскої пластинки, густина якої ![]() ?
?
14. Чому дорівнює
відцентровий момент інерції об’ємного тіла, густиною ![]() ?
?
15. Чому дорівнює кінетична енергія тіла яке обертається навколо осі я?
Розвяжіть самостійно.
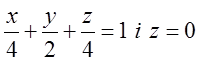 . Відп. 81/5.
. Відп. 81/5.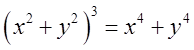 . Відп.
. Відп.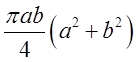 .
.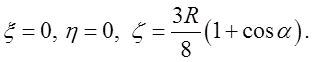
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.