CD: y=0;=> 0=r× sinj; r¹ 0 => sinj = 0; j = 0.
AB: y=x =>r sinj =r cosj; sinj =cosj; tgj=1 =>j=![]()
AD: x2+y2=2x =>r2cos2j + r2sin2j = 2r cosj; r2 = 2r cosj; r¹ 0 => r = 2 cos j;
BC: ![]() => r2 cos2j + r2 sinj = 4r cosj => r = 4 cosj;
=> r2 cos2j + r2 sinj = 4r cosj => r = 4 cosj;
Очевидно, що для того, щоб
одержати область ABCD
промінь з положення ![]() повинен переміститись в
положення
повинен переміститись в
положення ![]() (рівняння прямої АВ в полярній системі
координат). Під час цього переміщення
(рівняння прямої АВ в полярній системі
координат). Під час цього переміщення ![]() повинне
змінюватись від дуги кола
повинне
змінюватись від дуги кола ![]() до дуги кола
до дуги кола ![]() . Це і будуть границі інтегрування для
внутрішнього інтеграла.А тому маємо:
. Це і будуть границі інтегрування для
внутрішнього інтеграла.А тому маємо:
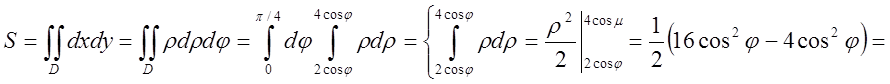
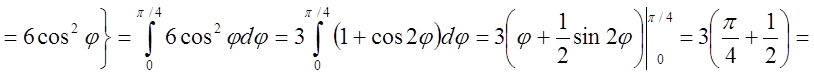
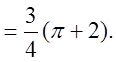 Відповідь:
Відповідь: 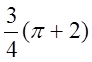
 П.2. Знайти
об`єм тіла, обмеженого параболоїдом 2аz = x2+y2 і
П.2. Знайти
об`єм тіла, обмеженого параболоїдом 2аz = x2+y2 і
сферою x2+y2+z2 = 3a2
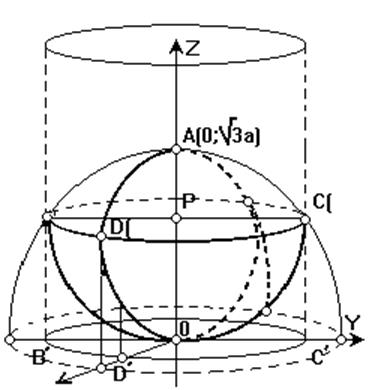
Розв’язок. Об’єм тіла будемо обчислювати через подвійний інтегрл. Зобразимо фігуру на рисунку (рис.6.2). Тіло, об`єм якого ми шукаємо, зверху
обмежене сферою BDCA а знизу параболоїдом BDCO, тому застосуємо (6.2).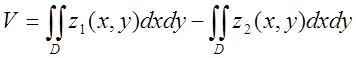 . Поверхні тіл перетинаються по
колу BDC, яке лежить на площині
паралельній площині XOY і віддаленій від неї на віддаль OP.
Рис.6.2.
. Поверхні тіл перетинаються по
колу BDC, яке лежить на площині
паралельній площині XOY і віддаленій від неї на віддаль OP.
Рис.6.2.
Знайдемо рівняння проекції
цього кола B¢D¢C¢ на площину XOY. Для цього нам треба
знайти радіус кола. Найлегше це можна зробити так: знаходимо координати точки С, розв`язуючи
систему 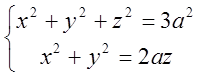 при х=0, так як С(0; yo; zo);
при х=0, так як С(0; yo; zo); 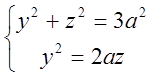 =>
2az + z2 = 3a2 ; z2 + 2az – 3a2 = 0; z1 = -3a; z2 = a;
=>
2az + z2 = 3a2 ; z2 + 2az – 3a2 = 0; z1 = -3a; z2 = a;
Із двох коренів підходить лише z2 = a; З рівняння 2az = x2+y2 при x = 0, y = a, знаходимо
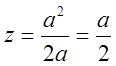 . Таким чином С(0;a;
. Таким чином С(0;a; ![]() ); C¢ (0; a; 0) рівняння кола B¢D¢C¢ буде x2+y2=a2.
); C¢ (0; a; 0) рівняння кола B¢D¢C¢ буде x2+y2=a2.
Очевидно, що 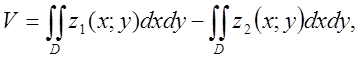 Де D– область, обмежена колом x2+y2=a2; z1 – функція рівняння сфери; z2 – функція рівняння параболоїда.
Очевидно, що
Де D– область, обмежена колом x2+y2=a2; z1 – функція рівняння сфери; z2 – функція рівняння параболоїда.
Очевидно, що
z2 = 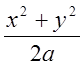 . Знайдемо в явному виді z1 з рівняння x2+y2+z2 = 3a2 => z = 3a2 - x2 - y2;
. Знайдемо в явному виді z1 з рівняння x2+y2+z2 = 3a2 => z = 3a2 - x2 - y2;
![]() так як у нас z > 0, то
так як у нас z > 0, то ![]() . Наявність виразуx2 + y2 і круговий вид області D спонукають нас до
заміни прямокутної системи координат на полярну. В зв`язку з симетричністю фігури
знайдемо її об`єм
лише для
. Наявність виразуx2 + y2 і круговий вид області D спонукають нас до
заміни прямокутної системи координат на полярну. В зв`язку з симетричністю фігури
знайдемо її об`єм
лише для 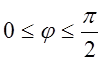 , а у відповіді запишемо результат в чотирі
рази більший.
, а у відповіді запишемо результат в чотирі
рази більший.
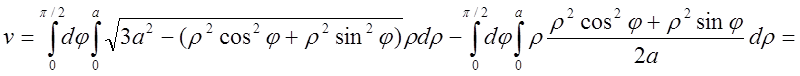
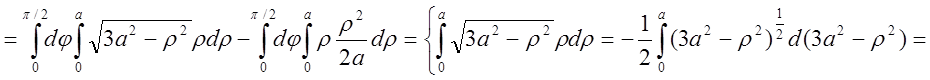
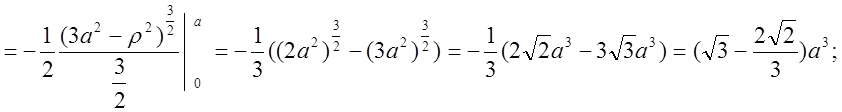
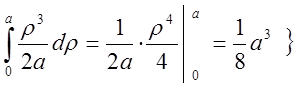 =
= 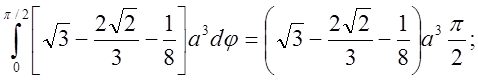
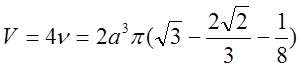 .
Відповідь:
.
Відповідь: 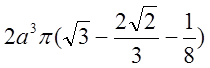 .
.
П.3. Обчислити площу поверхні частини сфери x2 + y2 + z2 =a2 , вирізаної циліндром x2 + y2 =ax,
Розв`язок. Застосуємо формулу (6.1а). Для того, щоб зобразити фігуру і визначити область інтегрування, перетворимо рівняння циліндра x2-ax+y2=0, виділивши повний квадрат.
|
|
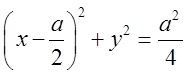 .Тепер очевидно, що цей
циліндр дотикається до осі OZйого вісь паралельна цій осі і проходить через точку С(
.Тепер очевидно, що цей
циліндр дотикається до осі OZйого вісь паралельна цій осі і проходить через точку С(![]() ; 0; 0). Проекція вирізаних циліндром частин сфери (їх буде
дві рис.6.3) на площину хОу матиме вид круга,
; 0; 0). Проекція вирізаних циліндром частин сфери (їх буде
дві рис.6.3) на площину хОу матиме вид круга,
Рис. 6.3. рівняння кола якого співпадає
з рівнянням напрямної циліндра, а сам круг зображено на рис.6.4. Це і буде
область інтегрування D. Верхня частина сфери в явному виді матиме рівняння ![]() . Похідні будуть
. Похідні будуть 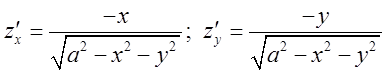 .
Підставимо ці значення в (6.1а)
.
Підставимо ці значення в (6.1а)
|
|
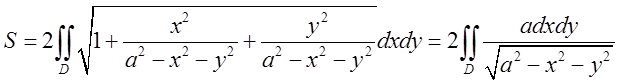 (*). Так, як область круг і підінтегральний вираз містить
(*). Так, як область круг і підінтегральний вираз містить ![]() , то доцільно перейти до полярноїсистеми
координат.
, то доцільно перейти до полярноїсистеми
координат.![]() . Так, як коло
. Так, як коло ![]() лежить
в півплощині
лежить
в півплощині ![]() , дотикаючись до вісі у, то,
розвязуючи нерівність
, дотикаючись до вісі у, то,
розвязуючи нерівність ![]() при
при ![]() ,
,
Рис.6.4. одержимо ![]()
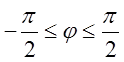 . Границі для
. Границі для ![]() дістанемо
перетворюючи нерівність, яка виражає круг, в полярну систему:
дістанемо
перетворюючи нерівність, яка виражає круг, в полярну систему: ![]()
![]() так, як
так, як ![]() не може бути відємним то з цієї нерівності
одержуємо
не може бути відємним то з цієї нерівності
одержуємо 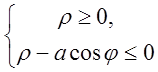 тобто границі для
тобто границі для ![]() будуть:
будуть:
![]() . Підставимо в (*).
. Підставимо в (*).
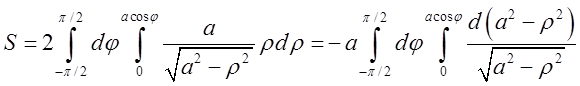 =
=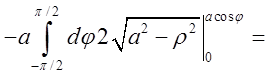
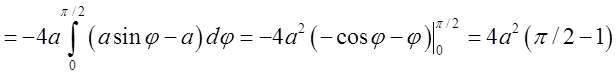
Відповідь. 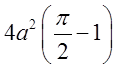 (одиниць кв.)
(одиниць кв.)
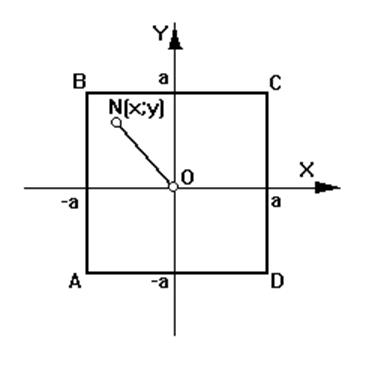 П.4. Знайти масу квадратної пластинки, сторона якої
дорівнює 2а, а поверхнева густина
П.4. Знайти масу квадратної пластинки, сторона якої
дорівнює 2а, а поверхнева густина ![]() в кожній точці
пропорційна квадрату її віддалі від точки перетику діагоналей і в вершинах
кутів дорівнює 1.
в кожній точці
пропорційна квадрату її віддалі від точки перетику діагоналей і в вершинах
кутів дорівнює 1.
Розв`язок. Використаємо формулу
(6.3) для знаходження маси 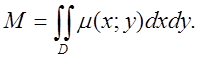
Пластинку в системі декартових координат розмістимо так, щоб початок системи координат знаходився в точці перетину діагоналей (рис.6.5.), Рис.6.5.
а сторони були паралельні осям
координат. Завдяки цьому будуть простими межі інтегрування. Область D – це квадрат ABCD. Візьмемо довільну точку N(x;y). ON2=x2+y2; тому m(x;y)=g(x2+y2), де g - коефіцієнт
пропорційності, який ми обчислимо з того, що в т. С(а; a) m =1 (згідно умови). 1=g(a2+a2), => g =![]() . Підставимо це в формулу обчислення мас і
враховуючи симетрію пластинки одержимо:
. Підставимо це в формулу обчислення мас і
враховуючи симетрію пластинки одержимо:
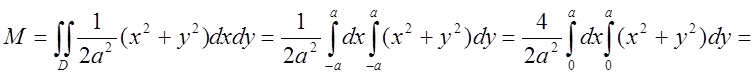
![]()
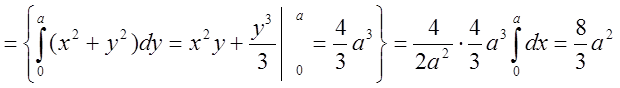 .
.
Відповідь:
П.5
Обчислити об’єм тіла заданого нерівностями : ![]() ;
; ![]() ;
; 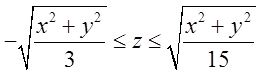 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.