Спеціальність Факультет МТ Семестр 11
Навчальна дисципліна Диференціальні рівняння (спеціальний курс)
1. Системи розв’язати
зведенням до одного рівняння п-го порядку, записавши де потрібно по заданій
матриці коефіцієнтів А відповідні системи 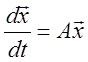 .
.
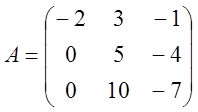
2. Розв’язати лінійні
однорідну систему 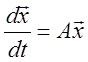 з наданою матрицею А методом
Ейлера.
з наданою матрицею А методом
Ейлера.
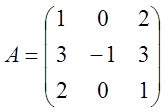
3. Розв’язати лінійні
однорідну систему 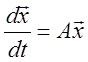 з наданою матрицею А матричним
методом.
з наданою матрицею А матричним
методом.
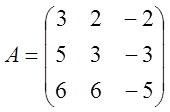
4. Розв’язати системи методом невизначених коефіцієнтів.
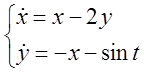
5. Розв’язати систему методом Лагранжа.
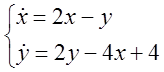
Затверджено на засіданні кафедри прикладної математики
Протокол № 5 от 5 березня 2004 р.
Зав. кафедрою проф. Грибанов В. М.
Екзаменатор Швед О. П.
Спеціальність Факультет МТ Семестр 11
Навчальна дисципліна Диференціальні рівняння (спеціальний курс)
1. Системи розв’язати
зведенням до одного рівняння п-го порядку, записавши де потрібно по заданій
матриці коефіцієнтів А відповідні системи 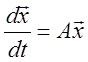 .
.
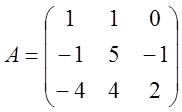
2. Розв’язати лінійні
однорідну систему 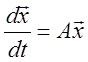 з наданою матрицею А методом
Ейлера.
з наданою матрицею А методом
Ейлера.
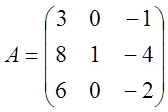
3. Розв’язати лінійні
однорідну систему 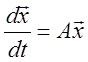 з наданою матрицею А матричним
методом.
з наданою матрицею А матричним
методом.
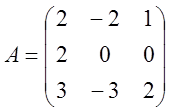
4. Розв’язати системи методом невизначених коефіцієнтів.
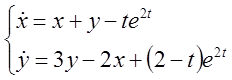
5. Розв’язати систему методом Лагранжа.
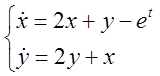
Затверджено на засіданні кафедри прикладної математики
Протокол № 5 от 5 березня 2004 р.
Зав. кафедрою проф. Грибанов В. М.
Екзаменатор Швед О. П.
Спеціальність Факультет МТ Семестр 11
Навчальна дисципліна Диференціальні рівняння (спеціальний курс)
1. Системи розв’язати
зведенням до одного рівняння п-го порядку, записавши де потрібно по заданій
матриці коефіцієнтів А відповідні системи 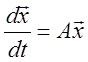 .
.
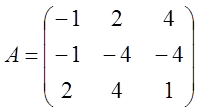
2. Розв’язати лінійні
однорідну систему 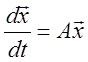 з наданою матрицею А методом
Ейлера.
з наданою матрицею А методом
Ейлера.
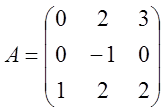
3. Розв’язати лінійні
однорідну систему 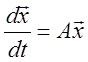 з наданою матрицею А матричним
методом.
з наданою матрицею А матричним
методом.
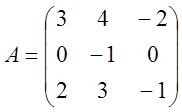
4. Розв’язати системи методом невизначених коефіцієнтів.
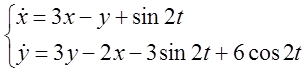
5. Розв’язати систему методом Лагранжа.
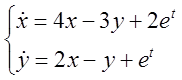
Затверджено на засіданні кафедри прикладної математики
Протокол № 5 от 5 березня 2004 р.
Зав. кафедрою проф. Грибанов В. М.
Екзаменатор Швед О. П.
Спеціальність Факультет МТ Семестр 11
Навчальна дисципліна Диференціальні рівняння (спеціальний курс)
1. Системи розв’язати
зведенням до одного рівняння п-го порядку, записавши де потрібно по заданій
матриці коефіцієнтів А відповідні системи 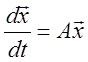 .
.
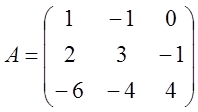
2. Розв’язати лінійні
однорідну систему 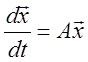 з наданою матрицею А методом
Ейлера.
з наданою матрицею А методом
Ейлера.
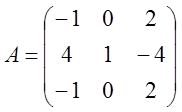
3. Розв’язати лінійні
однорідну систему 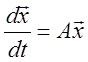 з наданою матрицею А матричним
методом.
з наданою матрицею А матричним
методом.
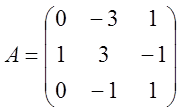
4. Розв’язати системи методом невизначених коефіцієнтів.
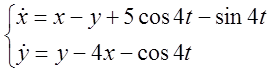
5. Розв’язати систему методом Лагранжа.
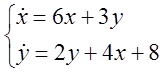
Затверджено на засіданні кафедри прикладної математики
Протокол № 5 от 5 березня 2004 р.
Зав. кафедрою проф. Грибанов В. М.
Екзаменатор Швед О. П.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.