Випадкові функції. Знаходження імовірностей станів і подій

Лабораторне заняття № 6

Задача 1. Розглядається випадкова функція , де  — центрована випадкова величина з дисперсією ;  — випадкова величина, розподілена з постійною щільністю в інтервалі , a  — невипадковий параметр . Випадкові величини  і  незалежні. Знайти характеристики випадкової функції : математичне чекання, кореляційну функцію. Визначити, чи є випадкова функція  стаціонарної і ергодичною. Якщо вона стационарна, то знайти її спектральну щільність .

Рішення. Представимо випадкову функцію  у виді

.

Позначимо ; . Знайдемо спочатку основні характеристики системи випадкових величин  і :

; ;

;

;

Тому що значення  розподілене рівномірно в інтервалі , те

;

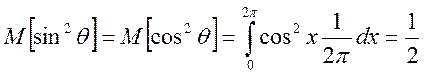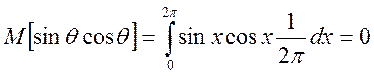
Отже, ; ; . Отже, вираження

являє собою спектральне розкладання стаціонарної випадкової функції: , а кореляційна функція має вигляд . Графік цієї функції показаний на мал. 1.

Ергодичною випадкова функція  не є, тому що характеристики, знайдені по одній реалізації, не збігаються з характеристиками, визначеними по безлічі реалізації. Дійсно, кожна реалізація випадкової функції  є гармонійне коливання, амплітуда якого являє собою значення, випадково прийняте величиною . Середнє за часом для кожної такої реалізації буде дорівнює нулеві і збігається з математичним чеканням випадкової функції , але дисперсія і кореляційна функція, знайдені як середні за часом для однієї реалізації, уже не будуть збігатися з відповідними характеристиками випадкової функції . Наприклад, .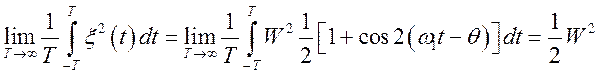

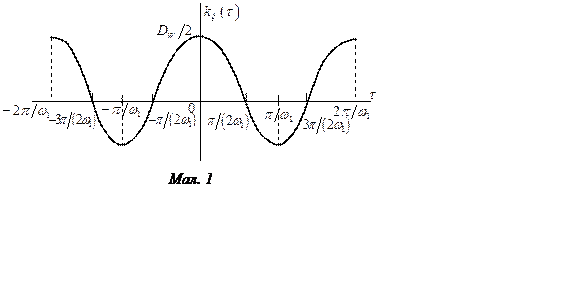Знайдемо спектральну щільність випадкової функції . Покажемо, що вона пропорційна дельта — функції:  . Дійсно, при такій спектральній щільності кореляційна функція

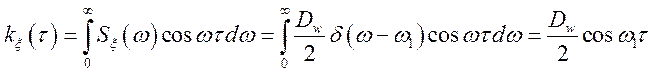
що збігається з кореляційною функцією для . А тому що пряме і зворотне перетворення Фур'є визначають спектральну щільність і кореляційну функцію взаємно — однозначно, те написане вище вираження для  дає спектральну щільність випадкової функції .

Якщо скористатися не дійсної, а комплексною формою перетворень Фур'є, одержимо спектральну щільність  у виді

 

Помітимо, що аналогічно можна було б записати і , але для позитивних  (тому що ) .

Задача 2. Система  — технічний пристрій, що складається з  вузлів і час від часу (у моменти ) підвергається профілактичному оглядові і ремонтові. Після кожного кроку (моменту огляду і ремонту) система може виявитися в одному з наступних станів:  — усі вузли справні (жоден не замінявся новим);  — один вузол замінений новим, інші справні;  — два вузли замінені новими, інші справні; ...;  вузлів  замінені новими, інші справні; ...;  — усі  вузлів замінені новими.

Імовірність того, що в момент профілактики вузол прийдеться замінити новим, дорівнює  (незалежно від стану інших вузлів). Розглядаючи стану системи  як марковський ланцюг, знайти перехідні імовірності і для ,  обчислити імовірності станів системи  після трьох кроків (у початковий момент усі вузли справні).

Рішення. Позначаючи , запишемо перехідні імовірності ланцюга. Для будь-якого стану системи   імовірність  дорівнює нулеві при ; імовірність  дорівнює імовірності того, що на даному кроці жоден вузол не прийдеться замінити новим, тобто  ще не замінених вузлів залишаються в складі пристрою: . При  імовірність переходу  дорівнює імовірності того, що на даному кроці з  ще не замінених вузлів  прийдеться замінити новими. Користуючись біноміальним розподілом, знаходимо . Стан  є поглинаючим. Для ,  граф станів системи має вигляд, показаний на мал. 2:

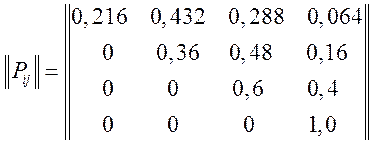
Маємо ; . Знаходимо імовірності станів після одного, двох, трьох кроків:

; ;

; ;

;

;

;

;

;

;

.

Задача 3. Крапка  «блукає» по осі абсцис  (мал. 3, а) по наступному законі: на кожнім кроці вона з імовірністю 0,5 залишається на місці, з імовірністю 0,3 перескакує на одиницю вправо і з імовірністю 0,2 — уліво. Стан системи  після  кроків визначається одною координатою (абсцисою) крапки . Початкове положення крапки — початок координат. Розглядаючи послідовність положень крапки  як ланцюг Маркова, знайти імовірність того, що вона після чотирьох кроків виявиться від початку координат не далі чим на відстані, рівній одиниці.

Рішення. Позначимо стан системи (крапки ) через , де  — координата  на осі абсцис. Розмічений граф станів по казан на малий. 3, б. (Отут для наочності проставлені «петлі», що відповідають затримці  в колишнім положенні.)

Послідовність станів утворить ланцюг Маркова з нескінченним числом станів. Перехідні імовірності  відмінні від нуля тільки у випадку ; ; ; ; ; . Всі інші перехідні імовірності дорівнюють нулеві. Шукана імовірність  дорівнює сумі імовірностей: . Знайдемо них, користуючись рекурентними співвідношеннями:  .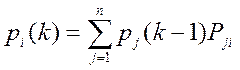

Маємо ; . Далі,

; ; ;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

.

Шукана імовірність

.

Отже, імовірність події , що складає в тім, що за чотири кроки крапка  виявиться від початку координат на відстані, не більшому одиниці, дорівнює 0,693.