Визначення стаціонарного випадкового процесу. Диференціювання стаціонарного випадкового процесу. Інтегрування стаціонарного випадкового процесу

Лекція 8

План:

1.  Визначення стаціонарного випадкового процесу.

2.  Диференціювання стаціонарного випадкового процесу.

3.  Інтегрування стаціонарного випадкового процесу.

1.  Визначення стаціонарного випадкового процесу

На практиці дуже часто зустрічаються випадкові процеси, що протікають у часі приблизно однородно і имеющие вид безперервних випадкових коливань навколо деякого середнього значення, причому ні середня амплітуда, ні характер цих коливань не виявляють існуючих змін з часом. Іншими словами, не простежується тенденція розвитку випадкових процесів у часі і, отже, при дослідженні стаціонарного процесу як відлік можна вибрати  будь-як момент часу.

Як приклади стаціонарних випадкових процесів можна привести: 1) коливання напруги в електричній освітлювальній мережі; 2) випадкові шуми в радіоприймачі; 3) процес хитавиці корабля і т.д.

Визначення. Випадковий процес  називається стаціонарним у вузькому змісті, якщо його багатомірні закони розподілу не міняються при зрушенні всіх тимчасових перемінних на те саме число.

 ,         (8.1)

Тоді

1. Одномірна щільність

        (8.2)

Отже одномірний закон розподілу  не залежить від часу, тобто однаковий по будь-якому перетині.

2. Двовимірний закон

;

                              (8.3)

Двовимірний закон розподілу залежить від різниці двох перемінних, тобто від довгі інтервалу  між перетинами випадкового процесу.

Для багатьох випадкових процесів мірний закон розподілу практично неможливо знайти. У багатьох прикладних задачах це і не потрібно. З досить високою точністю опис таких процесів можна здійснити, використовуючи одномірну і двовимірну щільність розподілу, тобто в межах кореляційної теорії.

По Хинчину процес  називається стаціонарним у широкому змісті, якщо:

1.

                       (8.4)

2.

,                 (8.5)

3.

                             (8.6)

Надалі кореляційну функцію стаціонарну в широкому змісті процесу будемо позначати .

Зі стаціонарності у вузькому змісті випливає стаціонарність процесу в широкому змісті. Зворотне невірне.

Надалі слова в «широкому змісті» будемо опускати.

Основні властивості стаціонарного процесу

1.

                                         (8.7).

Доказ.

Аналогічно формулі (8.2) запишемо:

, ,

але .

Якщо двовимірна функція розподілу четна, отже кореляційна функція — четна.

2.

                               (8.8).

3.

                              (8.9).

Доказ.

Т.к.

для стаціонарного процесу

, ,

тобто

.

Але

.

Отже,

.

Приклад.

,

де  і  — незалежні випадкові величини для яких виконуються рівності:

; ;

 — невипадкова величина. З'ясувати, чи стаціонарний процес.

Рішення.

,

,

 — стаціонарний.

Приклад.

Випадковий процес — узагальнений телеграфний сигнал.  Чи є він стаціонарним?

Рішення.

,

, .

 — процес стаціонарний.

2.   Диференціювання стаціонарного випадкового процесу

,  — стаціонарний випадковий процес.

Теорема. Перша похідна від стаціонарного процесу, є стаціонарний випадковий процес.

Доказ.

1.

,

,

.

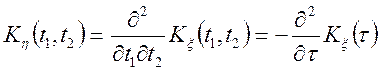Всі умови Хинчина виконані. Т.е. операція диференціювання стаціонарного процесу приводить до стаціонарного процесу. ч.т.д.

Приклад.

,

де  і  — невипадкові величини;  — випадкова величина, рівномірно розподілена на інтервалі ;

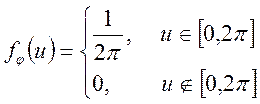
Знайти імовірностні характеристики похідної .

Рішення.

1.

  

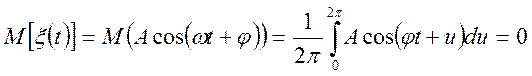
2.

, .

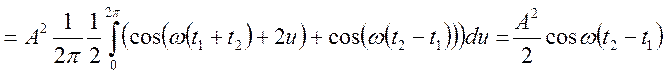
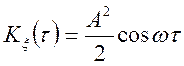2.

, ;

; .

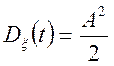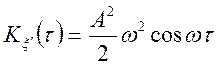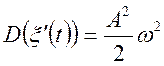Зауваження. Якщо розглядати  і безпосередньо обчислити імовірностні характеристики процесу , то вони збіжаться з раніше обчисленими характеристиками. Але в загальному випадку з диференційованості реалізацій не випливає диференційованість випадкового процесу і навпаки, диференційований випадковий процес може мати серед реалізацій не деференційовані (узагальнений телеграфний сигнал).

Справедлива

Теорема. Якщо випадковий процес диференціюємо, то його реалізації з імовірністю рівній одиниці, є безперервними функціями.

Приклад.

Дано послідовність прямокутних імпульсів не рівних одиниці, причому зміна їхніх значень приходить у випадкові моменти часу, що утворять пуасоновський потік (узагальнений телеграфний сигнал). Показати, що такий процес не диференціюємо.

Рішення.

,

.

У крапці   не існує.

Якщо диференціювання стаціонарного процесу приводить до стаціонарного процесу, то інтегрування не завжди.

3.  Інтегрування стаціонарного випадкового процесу

Нехай випадковий процес 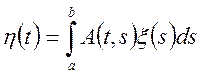 інтегруємо,  — ядро, при цьому процес  — стаціонарний у широкому змісті, тобто

, , ,

те характеристики випадкового процесу 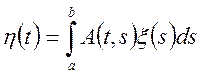 наступні:

,

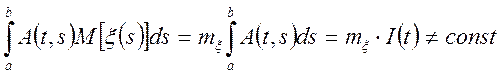т.е. умови стаціонарності порушуються.

Якщо зажадати, що  — стаціонарний і центрований , тобто , то

,

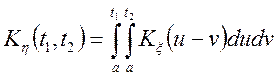цей інтеграл у загальному виді не повинний залежати від .

Звичайно існують умови, при виконанні яких інтегрування стаціонарного процесу приводить до стаціонарного процесу. Допустимо, виконуються умови:

1. ;

2.

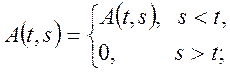
3. Нижня межа інтегрування , тоді інтеграл від , тобто процес  буде стаціонарним.

Доказ.

;

,

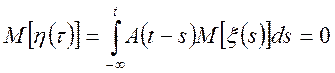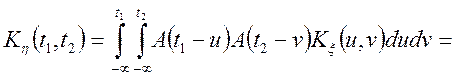
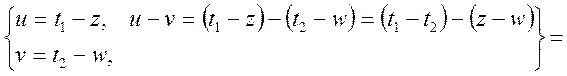
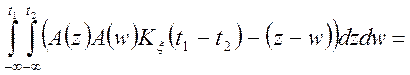
що і було потрібно довести.