


Лабораторне заняття № 3
Задача 1. Визначити середнє
квадратичне відхилення кута ![]() поворот гіроскопа
напрямку після 10 хв. роботи гіроскопа внаслідок наявності випадкового
моменту
поворот гіроскопа
напрямку після 10 хв. роботи гіроскопа внаслідок наявності випадкового
моменту ![]() , що виникає на осі внутрішнього карданова
кільця, якщо рівняння, що визначає закон зміни
, що виникає на осі внутрішнього карданова
кільця, якщо рівняння, що визначає закон зміни ![]() , може
бути прийняте у виді
, може
бути прийняте у виді ![]() =
=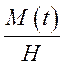 , де
кінетичний момент
, де
кінетичний момент 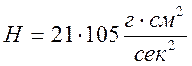 , а
, а 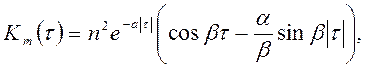
n=1,36·104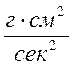 , β=0,7 сек.-1, α=0,1
сек.-1.
, β=0,7 сек.-1, α=0,1
сек.-1.
Рішення. Тому що після інтегрування маємо (початкові умови, у відповідності зі змістом задачі, нульові)
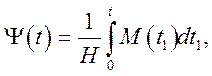 , тобто
, тобто ![]() зв'язана з
зв'язана з ![]() лінійним
співвідношенням, то для кореляційної функції
лінійним
співвідношенням, то для кореляційної функції ![]() одержимо
одержимо
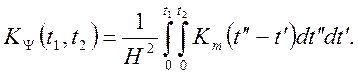
а для дисперсії 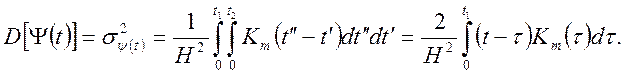
Тому що
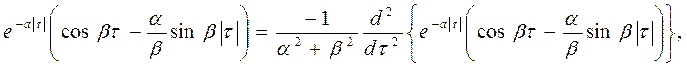
те останній інтеграл просто може бути обчислений вроздріб, що дає
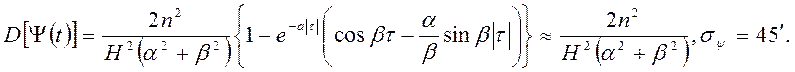
Задача 2. Характеристики похідної
випадкового процесу. Мається випадковий процес ![]() з
математичним чеканням
з
математичним чеканням ![]() і кореляційною функцією
і кореляційною функцією ![]() . Знайти характеристики
. Знайти характеристики ![]() ,
, ![]() і
і ![]() її похідній
її похідній ![]() .
Знайти також взаємну кореляційну функцію
.
Знайти також взаємну кореляційну функцію ![]() .
.
Рішення. Випадкова функція ![]() зв'язана з
зв'язана з ![]() лінійним
однорідним перетворенням. Застосовуючи загальні правила (1.7), (1.8), (1.9),
одержуємо:
лінійним
однорідним перетворенням. Застосовуючи загальні правила (1.7), (1.8), (1.9),
одержуємо:
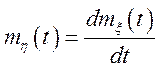 ;
; 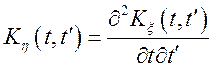 ;
; 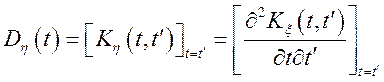 ;
; 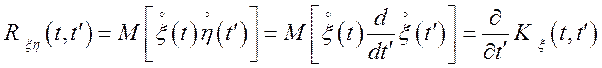 .
.
Помітимо, що 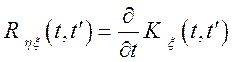 .
.
Задача 3. Характеристики інтеграла
від випадкового процесу. Мається випадковий процес ![]() і
дані його характеристики:
і
дані його характеристики: ![]() ,
, ![]() . Знайти характеристики
. Знайти характеристики ![]() ,
, ![]() інтеграла
цього випадкового процесу
інтеграла
цього випадкового процесу 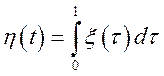 , а також взаємну
кореляційну функцію
, а також взаємну
кореляційну функцію ![]() .
.
Рішення. 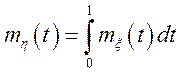 ;
; 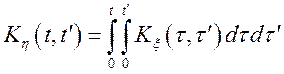 ;
; 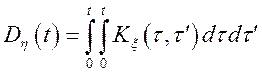 ;
;
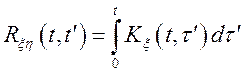
Помітимо, що 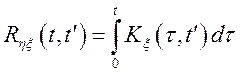 .
.
Можна довести, що не існує відмінної
від нуля випадкової функції ![]() , при якій
, при якій ![]() стационарна.
стационарна.
Задача 4. Випадкова функція ![]() з характеристиками
з характеристиками ![]() ,
,
![]() піддається лінійному, перетворенню виду
піддається лінійному, перетворенню виду 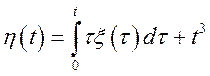 . Визначити характеристики випадкової
функції
. Визначити характеристики випадкової
функції ![]() :
: ![]() ,
, ![]() .
.
Рішення. 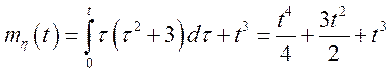 .
.
Однорідна частина розглянутого
лінійного перетворення 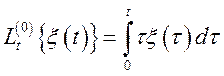 .
.
Отже, 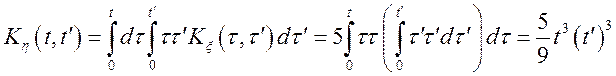 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.