


Лабораторне заняття № 1
Задача 1. Визначити математичне чекання і кореляційну функцію випадкової функції
![]()
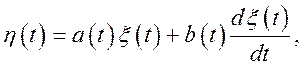
де a(t) і b(t)
— задані (числові) функції, ![]() — диференційована
випадкова функція, a
— диференційована
випадкова функція, a ![]() (t) і
(t) і ![]() відомі.
відомі.
Рішення. Функція ![]() є результатом застосування лінійного
оператора
є результатом застосування лінійного
оператора 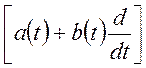 до випадкової функції
до випадкової функції ![]() . Тому шуканий результат може бути
отриманий шляхом застосування загальних формул. Однак рішення простіше знайти
шляхом безпосереднього обчислення
. Тому шуканий результат може бути
отриманий шляхом застосування загальних формул. Однак рішення простіше знайти
шляхом безпосереднього обчислення ![]() (t) і
(t) і ![]() . Маємо
. Маємо
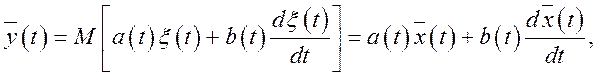
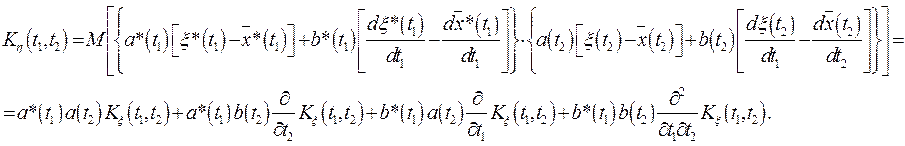
Задача 2. Визначити кореляційну
функцію ![]() , якщо
, якщо
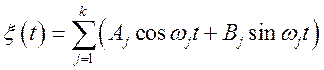 ,
,
де ![]() —
задані числа, а речовинні випадкові величини
—
задані числа, а речовинні випадкові величини ![]() і
і ![]() , взаємно не кореліровані, мають нульові
математичні чекання і дисперсії, обумовлені рівностями
, взаємно не кореліровані, мають нульові
математичні чекання і дисперсії, обумовлені рівностями
![]() (j=1,2,…,k)...
(j=1,2,…,k)...
Рішення. Тому що 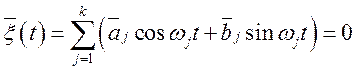 , те по визначенню кореляційної функції
, те по визначенню кореляційної функції
![]()
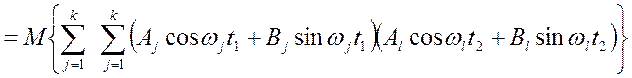 .
.
Розкриваючи дужки і застосовуючи
теорему про математичне чекання, зауважуємо, що всі доданки, що містять
множники виду ![]() при j≠ l і
при j≠ l і ![]() при будь-яких j і l
дорівнюють нулеві, а
при будь-яких j і l
дорівнюють нулеві, а ![]() . Тому
. Тому
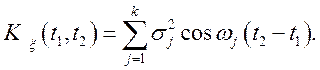
Задача 3. ВВ є часткою случаємо такої
випадкової функції, у якого відсутня залежність від часу ![]() й описується показовим законом розподілу,
з
й описується показовим законом розподілу,
з ![]() =2 (
=2 ( ![]() ).
Знайти:
).
Знайти: ![]()
![]()
![]()
Рішення.Відсутність перемінної ![]() вказує на те, що усі імовірностні
характеристики не будуть від неї залежати.
вказує на те, що усі імовірностні
характеристики не будуть від неї залежати.
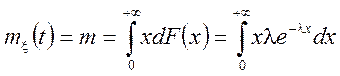 =( інтегруючи вроздріб, маємо )=
=( інтегруючи вроздріб, маємо )=![]() ;
;
аналогічно для дисперсії 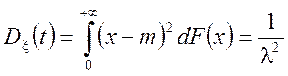 .
.
![]() .
.
Звідси легко бачити, що 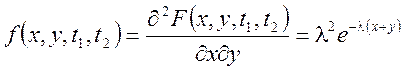
Задача 4. Двовимірний закон розподілу
випадкової величини ( надалі ВВ ) ![]() записується
щільністю:
записується
щільністю:
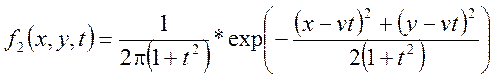
Знайти усі імовірностні характеристики.
Рішення. Знайдемо одномірну щільність розподілу:
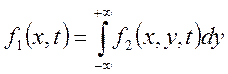 =
=![]() розділяючи
перемінні і виносячи константи за знак інтеграла маємо
розділяючи
перемінні і виносячи константи за знак інтеграла маємо![]() =
=
=
=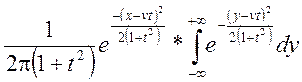 =
=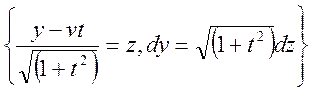 =
=
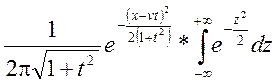 =
=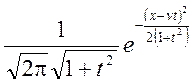 .
.
Ця щільність описує нормальний
розподіл з параметрами ![]()
У даному випадку дисперсію не можна
обчислювати як ![]() , тому що випадковий процес є
некорелірованим,т.е
, тому що випадковий процес є
некорелірованим,т.е ![]()
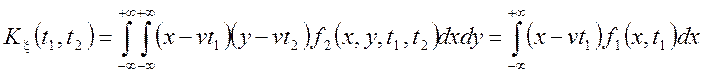
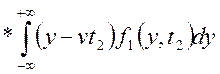 =
=![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.