Специальность 80202-прикладная математика
по дисциплине "Теория управления"
Задача 1. Анализ системы управления.
Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
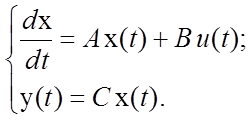
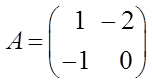 ;
; 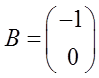 ;
;  .
.
Исследовать управляемость и наблюдаемость системы.
Построить импульсную переходную матрицу системы, используя преобразования Лапласа.
Задача 2. Метод классического вариационного исчисления.
Линейная система управления описывается следующим дифференциальным уравнением:
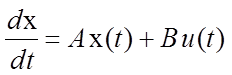 ,
,
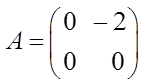 ;
; 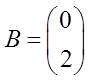 .
.
Определить оптимальный процесс перевода системы из
точки ![]() ,
, ![]() в
точку
в
точку ![]() фазового пространства за отрезок времени
фазового пространства за отрезок времени ![]() , затрачивая при этом минимум энергии, т.е.
, затрачивая при этом минимум энергии, т.е.
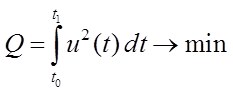 .
.
Задача 3. Принцип максимума Понтрягина.
Система управления описывается дифференциальным уравнением:
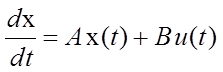 ,
,
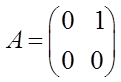 ,
, 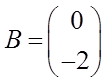 .
.
Требуется определить управление ![]() , обеспечивающее быстрейший перевод системы
из состояния
, обеспечивающее быстрейший перевод системы
из состояния ![]()
![]() в
начало координат
в
начало координат ![]() при условии, что управление
должно удовлетворять ограничению
при условии, что управление
должно удовлетворять ограничению ![]() .
.
Построить фазовые траектории системы управления.
Преподаватель …………………… доц. НЕФЕДОВ Ю М.
Специальность 80202-прикладная математика
по дисциплине "Теория управления"
Задача 1. Анализ системы управления.
Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
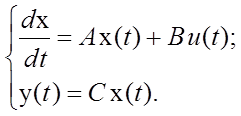
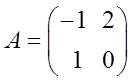 ;
; 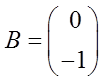 ;
; 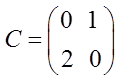 .
.
Исследовать управляемость и наблюдаемость системы.
Построить импульсную переходную матрицу системы, используя преобразования Лапласа.
Задача 2. Метод классического вариационного исчисления.
Линейная система управления описывается следующим дифференциальным уравнением:
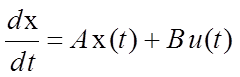 ,
,
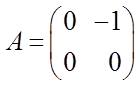 ;
; 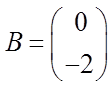 .
.
Определить оптимальный процесс перевода системы из
точки ![]() ,
, ![]() в
точку
в
точку ![]() фазового пространства за отрезок времени
фазового пространства за отрезок времени ![]() , затрачивая при этом минимум энергии, т.е.
, затрачивая при этом минимум энергии, т.е.
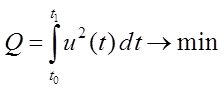 .
.
Задача 3. Принцип максимума Понтрягина.
Система управления описывается дифференциальным уравнением:
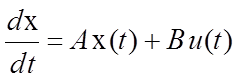 ,
,
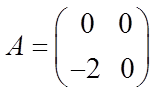 ,
, 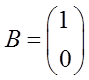 .
.
Требуется определить управление ![]() , обеспечивающее быстрейший перевод системы
из состояния
, обеспечивающее быстрейший перевод системы
из состояния ![]()
![]() в
начало координат
в
начало координат ![]() при условии, что управление
должно удовлетворять ограничению
при условии, что управление
должно удовлетворять ограничению ![]() .
.
Построить фазовые траектории системы управления.
Преподаватель …………………… доц. НЕФЕДОВ Ю М.
Специальность 80202-прикладная математика
по дисциплине "Теория управления"
Задача 1. Анализ системы управления.
Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
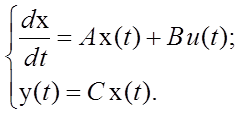
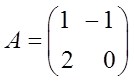 ;
; 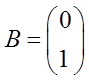 ;
; 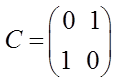 .
.
Исследовать управляемость и наблюдаемость системы.
Построить импульсную переходную матрицу системы, используя преобразования Лапласа.
Задача 2. Метод классического вариационного исчисления.
Линейная система управления описывается следующим дифференциальным уравнением:
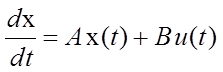 ,
,
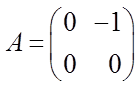 ,
, 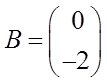 .
.
Определить оптимальный процесс перевода системы из
точки ![]() ,
, ![]() в
точку
в
точку ![]() фазового пространства за отрезок времени
фазового пространства за отрезок времени ![]() , затрачивая при этом минимум энергии, т.е.
, затрачивая при этом минимум энергии, т.е.
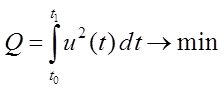 .
.
Задача 3. Принцип максимума Понтрягина.
Система управления описывается дифференциальным уравнением:
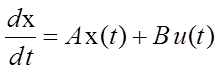 ,
,
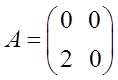 ,
,  .
.
Требуется определить управление ![]() , обеспечивающее быстрейший перевод системы
из состояния
, обеспечивающее быстрейший перевод системы
из состояния ![]()
![]() в
начало координат
в
начало координат ![]() при условии, что управление
должно удовлетворять ограничению
при условии, что управление
должно удовлетворять ограничению ![]() .
.
Построить фазовые траектории системы управления.
Преподаватель …………………… доц. НЕФЕДОВ Ю М.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.