Excel, аппроксимация, страница 5

Рис. 10.1-3

Рис. 10.1-4

Таким образом, при Х=12 ожидается Y=9,44, а при Х=4,5; Y=4,66.

Используя значения X и Y с помощью Excel, построим график, совмещенный с линией регрессии (линией тренда), как показано на рис. 10.1-4.

@ В Excel имеется очень простой способ строить линейную аппроксимацию равноотстоящих значений аргумента. Для этого нужно выделить известные значения прогнозируемой величины и потянуть за маркер заполнения, удерживая правую кнопку мыши. Затем, из появившегося контекстного меню (его фрагмент приведен на рис. 10.1-5) выбрать пункт Линейное приближение. В заполняемых клетках мы обнаружим значения, вычисленные системой для найденного ею линейного уравнения регрессии.

			Рис. 10.1-5

 

На рис.10.1-6 исходными значениями являются 2, 4, 5. Остальные числа являются вычисленным прогнозом в предположении линейной связи аргументов в соответствии с найденным Excel уравнением.

2

4

5

6,67

8,17

9,67

11,17

12,67

Рис. 10.1-6

Здесь же (рис.10.1-7), при необходимости, можно выбрать и Экспоненциальное приближение.

2

4

5

8,55

13,52

21,37

33,80

53,44

Рис. 10.1-7

Графическое отображение обеих кривых представлено на рис. 10.1-8.

 

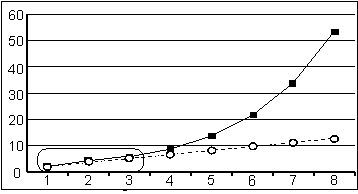Рис. 10.1-8

С помощью средств деловой графики Excel можно не только построить необходимые кривые, но получить линии тренда и соответствующие им уравнения Y(X) (здесь y=1,5x+0,6667 для линейного закона, y=1,368e0,4581x – для экспоненты). Экспоненциальная аппроксимация обозначена прямоугольными точками, линейная – кружками. Исходные точки обведены овалом.

10.2. Полиномиальнаяаппроксимация

Видим (рис. 10.1-4), что, хотя уравнение регрессии правильно отражает направление роста функции, оно является достаточно грубым приближением. Здесь необходимо воспользоваться более сложной аппроксимирующей функцией. В качестве таких функций чаще всего используют степенные полиномы разной степени вида