1.4. Класс точности приборов
Всем выпускаемым промышленностью измерительным приборам присваивается класс точности. Он устанавливается при метрологических обследованиях выпускаемой серии и является, прежде всего, характеристикой серии, а не конкретного прибора.
Под классом точности подразумевается наибольшая относительная погрешность прибора в нормальных условиях работы. Относительная погрешность, равная классу точности, оценивается по выражению:
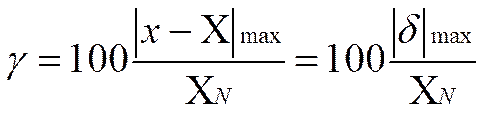 ; (1.2)
; (1.2)
где: х – измеренное значение физической величины;
Х – истинное значение физической величины, полученное с помощью образцового прибора;
׀δ ׀ max –наибольшая по модулю абсолютная погрешность измерения;
XN–рабочая часть шкалы прибора (в приборах с двухсторонним отсчётом учитывается вся шкала).
Относительная погрешность каждого прибора серии должна находиться в пределах его класса точности.
Классы точности приборов: 0,005; 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,4; 4,0. Они указываются обычно на шкале прибора. Соответствующие условия работы поясняются в паспорте. Технические приборы имеют классы точности: 0,5;1,0; и т.д.; на лабораторные – от 0,005 до 0,2.
1.5. Оценка погрешности измерения
Результаты измерения всегда приближены, поскольку содержат те или иные погрешности. Основная задача при измерении – получать оценку результата, наиболее близкую к истинному значению. Для этого требуется найти погрешность измерения и уточнить результат поправкой.
В практике измерений для оценки погрешностей есть два подхода (метода).
Один подход – грубый, предназначен для одноразовых измерений. Он связан с использованием паспортных данных о классе точности прибора. Проведя измерение и зная класс точности прибора, можно указать, в каком пределе находится истинное значение измеряемой величины. Из соотношения (1.1) получим:
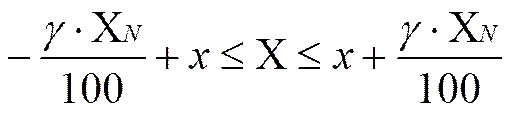 . (1.3)
. (1.3)
Грубый подход позволяет оценить диапазон истинных значений. Это связано с тем, что в выражении (1.3) уже заданы возможные допустимые значения погрешностей. Для технических приборов такие оценки вполне достаточны и, если при проверке с образцовыми приборами их погрешности находятся в пределах нормы, то показания прибора принимаются за истинные.
Имеется и другой, более точный подход к оценке погрешностей измерения. Он основан на использовании методов математической статистики и может быть реализован в тех случаях, когда имеется возможность получить несколько измерений одной и той же величины.
Методы статистики не позволяют выявить систематические погрешности. Поэтому при оценке случайных погрешностей обычно полагают, что систематические погрешности отсутствуют.
Для оценки случайных погрешностей по этому подходу нужно иметь достаточно большое количество разовых измерений установившейся величины или запись их на диаграммную ленту.
Теоретически и экспериментально доказано, что при большом числе наблюдений можно считать, что значения случайных величин распределяются по нормальному закону К.Ф. Гаусса.
Нормальный закон распределения погрешностей имеет вид:
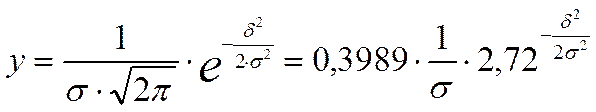 (1.4)
(1.4)
где: y–плотность распределения;
δ=х-Х – абсолютная погрешность измерения;
σ–средняя квадратическая погрешность. Средняя квадратическая погрешность характеризует величину рассеяния отдельных погрешностей от величины Х.
при обработке результатов измерения, содержащих случайные погрешности, истинное значение Х определяется приближенно по среднеарифметическому значению х ряда измерений:
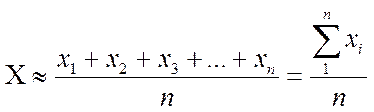 , (1.5)
, (1.5)
где: n–число измерений;
хi–результат i-го измерения.
Приближенное значение средней квадратической погрешности
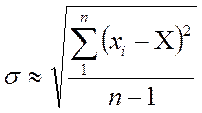 . (1.6)
. (1.6)
Для уточнения истинного значения результата вычисляется ещё доверительный интервал. Величина Х заданной заранее доверительной вероятностью при определённом числе измерений n лежит в интервале:
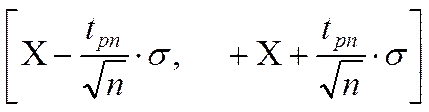 , (1.7)
, (1.7)
где tpn–Коэффициент Стьюдента, который находят из таблиц, составленных с помощью так называемого распределения Стьюдента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.