Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
По дисциплине ______________ЭММ_______________________________________
________________________________________________________________________
(наименование учебной дисциплины согласно учебному плану)
Тема: Оптимальное распределение ресурсов
Автор: студент гр. ГК-00 ____________________ /Симонова М. С./
(подпись) (Ф.И.О.)
Дата: ___________________
ПРОВЕРИЛ __доцент__ ________________ /Беляев В. В./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2003 год
Вариант №8
Задание: Составить план выпуска продукции предприятия. Цель планирования – достижение максимальной прибыли.
Считать единицу измерения объема выпуска достаточно большой
(например, тысячи штук) – т.е. результат не обязательно целый.
Отчет о выполнении лабораторной работы №4 содержит:
1. Условие
2. Постановку задачи. Формулировку задачи ЛП. (MS Equation)
3. Решение задачи на MS Excele. которая включает:
· решение (1) исходной задачи
· решение задачи с введением дополнительных переменных – неиспользованных ресурсов (остатков)
· решение двойственной задачи
4. Экономический анализ полученных результатов решения (1)
· Структура полученного решения выводы о видах продукции, которые целесообразно или нецелесообразно выпускать
· Сведения о полностью использованных ресурсах и о ресурсах, по которым имеются остатки. Сформулировать рекомендации по их использованию
· Для каждого вида продукции определить диапазон изменения величины прибыли от реализации единицы продукции, в котором структура оптимального выпуска сохраняется.
· Для каждого вида ресурса определить диапазон изменения величины фактического наличия ресурса, в котором структура оптимального выпуска сохраняется.
· Определить характер изменения суммарной прибыли принудительном выпуске продукции, не вошедшей в оптимальный план выпуска.
· Определить характер изменения величины прибыли при изменении величины фактического наличия ресурса. ( Использовать значение «Теневой цены»)
Для этого получить отчеты в MS Excele
· По результатам
· По устойчивости
· По пределам
5. Отчет о двойственной задаче должен содержать выводы о совпадении
· значении ЦФ прямой и двойственной задач
· о симметричности решения прямой и двойственной задач по «теневым ценам» и значениям искомых переменных
6. Отчет о решении(2) задачи должен содержать выводы и сравнения с решением(1)
· о совпадении значений ЦФ
· о сопоставлении использованных ресурсов и остатков
· о совпадении по «теневым ценам» и значениям искомых переменных
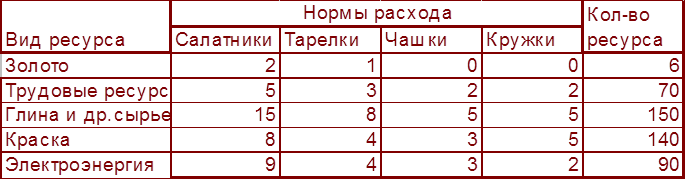
Условие: Предприятие может производить продукцию следующих видов салатники, тарелки , чашки и кружки. Реализация одной единицы каждого вида продукции дает прибыль в 15, 7, 5 и 4 условных единиц соответственно. Перечень ресурсов, их количество и нормы расхода для производства единицы продукции каждого вида приведено в таблице 1.
Исходные данные задачи распределения ресурсов
Табл.1
Решение:
Составим математическую модель для данной задачи. Пусть хj – количество выпускаемой продукции j-ого типа, j=1,2,3,4. Как видно из таблицы 1, для выпуска одного салатника требуется 2 единицы золота, значит, для выпуска всего количества салатников требуется 2х1 единиц золота, для выпуска всего количества тарелок требуется 1х2 единиц золота и т.д. Таким образом, ограничения по золоту будет иметь вид: 2х1+1х2+0х3+0х4≤6. В этом ограничении левая часть показывает потребность в ресурсе (затраты золота на производство продукции в объемах х1,х2, х3, х4), а правая – его имеющиеся количества в наличии.
Аналогично можно составить ограничения для других ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь следующий вид:
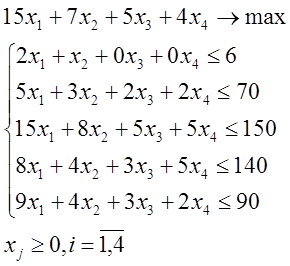 - фазовые ограничения
- фазовые ограничения
естественное ограничение
Решение в Excel с помощью надстройки «Поиск
решения»
1. Разместим на рабочем листе MS Excel исходные данные, как показано на рис. 1: в ячейках В6:Е6 значение переменных положим равным 0, в ячейке F7 значение целевой функции вычисляется по формуле =СУММПРОИЗВ (В6:Е6; В7:Е7). Левая часть ограничений вычислена следующим образом: в ячейку F10 занесена формула =СУММПРОИЗВ ($B$6:$E$6; B10:E10), после чего она скопирована в ячейки F11:F14.
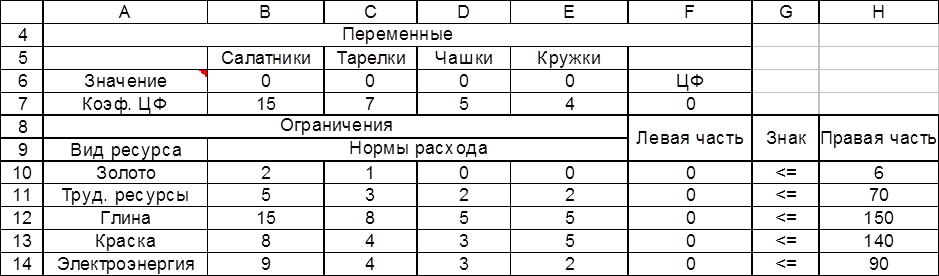
рис. 1
2. Активизируем настройку «поиск решения». Из пункта меню «Сервис» и заполним диалоговое окно, как показано на рис. 2.(в «параметрах» «поиска решения» обязательно отметим линейность модели). Нажмем на кнопку «выполнить».
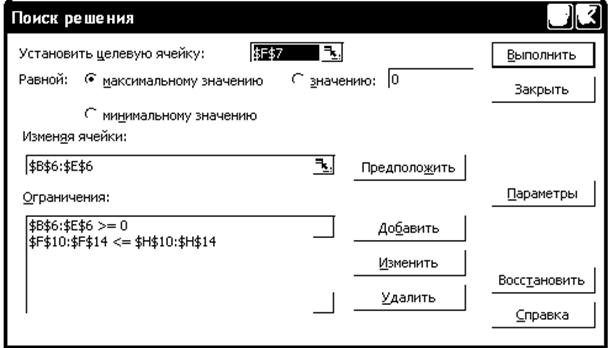
рис. 2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.