Решение задачи об оптимальном распределении ресурсов симплекс методом, при помощи надстройки Excel «Поиск решения» с введением и без введения дополнительных переменных. Решение двойственной задачи, составленной к исходной

Министерство образования Российской Федерации

Санкт-Петербургский Государственный Горный Институт им. Г.В. Плеханова

(Технический Университет)

Кафедра информатики и

 компьютерных технологий

Предмет: Экономико-математические методы

Лабораторная работа №4

Решение задачи об оптимальном распределении ресурсов симплекс методом, при помощи надстройки Excel «Поиск решения» с введением и без введения дополнительных переменных. Решение двойственной задачи, составленной к исходной.

                                                                                        Выполнила: ст. гр. ГК-01Чеснокова О.Г.                                                      

                                                                                         Проверил: доцент Беляев В. В.                                                                                      

Санкт-Петербург

2004

                                          Вариант 10.

Предприятие проводит капитальный ремонт и реконструкцию жилого фонда:

·  кирпичные здания исторической застройки

·  кирпичные здания рядовой застройки

·  памятники архитектуры

·  модернизация «хрущевок».

 Реализация единицы жилой площади каждого вида застройки дает прибыль в 10, 8, 6 и 6  условных единиц соответственно. Перечень ресурсов, их количество  и нормы расхода для производства единицы жилой площади каждого вида застройки приведены в таблице 1.1

      Таблица 1.1

Вид ресурса	Нормы расхода				Кол-во ресурса
	историческая застройка	рядовая застройка	памятники архитектуры	модернизация «хрущевок»
электроэнергия	1	3	2	2	35
трудовые ресурсы	1	2	2	2	30
кирпич	10	10	7	5	300
бетон	5	2	10	8	100
металлоконструкции	5	6	5	1	75

                             Решение:

 Составим математическую модель для данной задачи. Пусть x_j – количество выпускаемой продукции j-го типа, j=1,2,3,4. Как видно из таблицы 1.1, для капитального ремонта и реконструкции одного квадратного метра кирпичного здания исторической застройки  требуется 1 единица электроэнергии, значит, для капитального ремонта всего кирпичного здания исторической застройки потребуется 1 x₁ единиц электроэнергии, для реконструкции всего кирпичного здания рядовой засройки потребуется 3 x₂ единиц электроэнергии  и т.д. Таким образом, ограничение по электроэнергии будет иметь вид: 1 x₁+3 x₂+2 x₃+2 x₄£35. В этом ограничении левая часть показывает потребность в ресурсе (затраты электроэнергии на строительство жилья в объемах x₁, x₂, x₃, x₄), а правая – его имеющееся количество в наличии.

Аналогично можно составить ограничения для других ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь следующий вид:

 

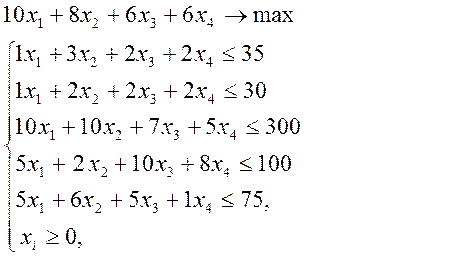
Задача может быть решена симплекс-методом.