Задание 1.
Задание: Найти преобразование Фурье и построить спектр
периодической функции.
Исходные данные:
Функция задана графически.
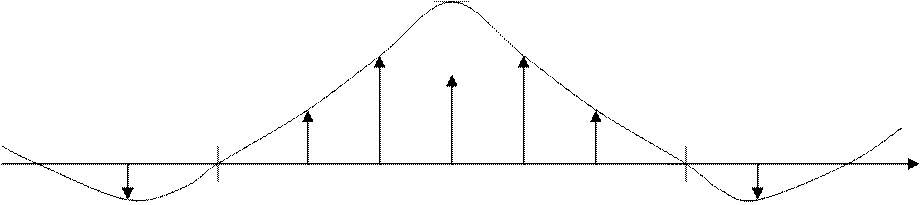
Рис. 1. Исходная функция
Из рисунка 1 видно, что исходный график похож на меандр. Только у меандра
соотношение периода к длительности (т.е. скважность) равно 2, а в исходном
графике скважность равна 3. Т.е. можно сказать , что у известного нам меандра
увеличили период в 1.5 раза, то тогда по свойствам преобразования Фурье и руководствуясь
здравым смыслом, можно сказать, что при увеличении периода меандра его спектр
будет «сужаться».
Приведем исходную функцию к гармоническому ряду Фурье:
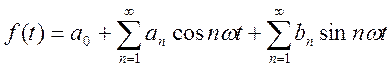 , где n=1,2,3…
, где n=1,2,3…
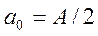 , где А – амплитуда
, где А – амплитуда
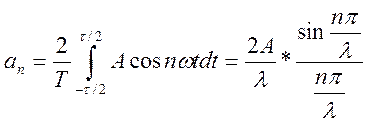 , где l - скважность.
, где l - скважность.
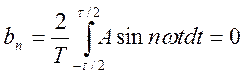
Сделаем расчеты спектров для построения отcчетной
функции:
Таблица 1. Расчет значений.
|
Значения n
|
спектры
|
Приблизительные
значения при А=1
|
|
0
|
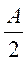
|
0,5
|
|
1
|
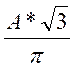
|
0,55
|
|
2
|
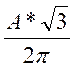
|
0,28
|
|
3
|
0
|
0
|
|
4
|
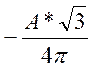
|
-0,13
|

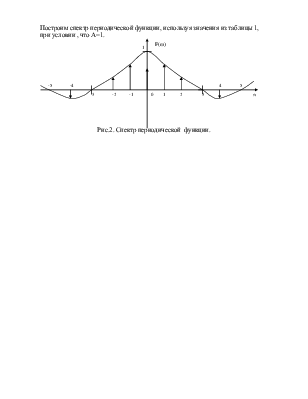
Построим спектр периодической функции,
используя значения из таблицы 1, при условии , что А=1.
Рис.2. Спектр периодической функции.
Задание 2.
Исходные данные:
Кодовая комбинация: 1000
Схема: Б
Ошибка в пятом разряде.
Найти:
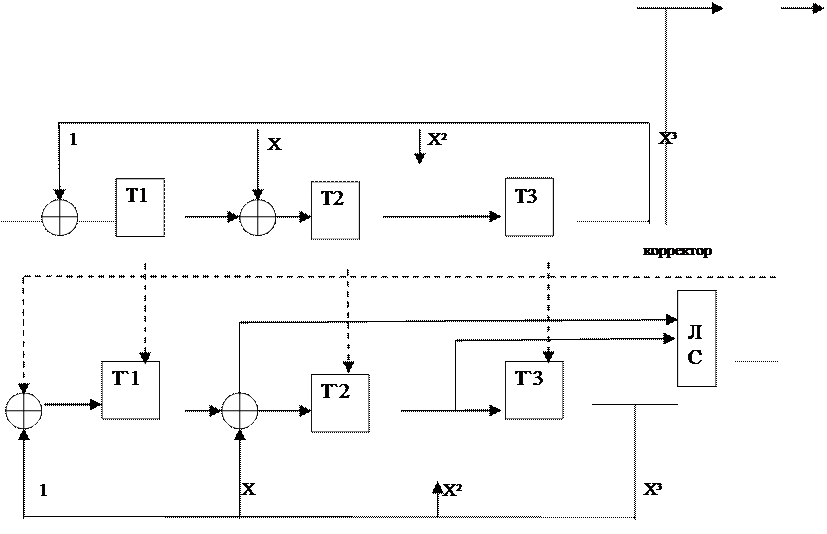
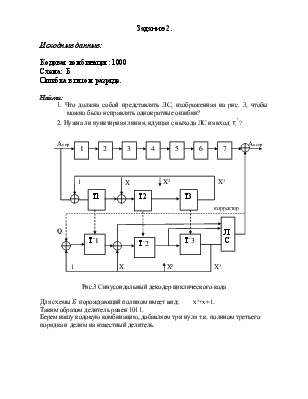
1. Что должна собой представлять ЛС,
изображенная на рис. 3, чтобы можно было исправлять однократные ошибки?
2.
Нужна ли пунктирная линия, идущая с выхода ЛС на вход 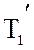 ?
?





Рис.3 Синусоидальный декодер циклического кода
Для схемы Б порождающий
полином имеет вид: x³+x+1.
Таким образом делитель равен
1011.
Берем нашу кодовую комбинацию, добавляем три нуля т.к.
полином третьего порядка и делим на известный делитель.
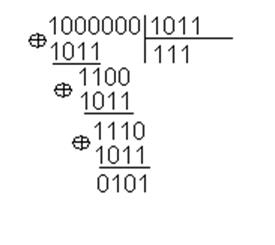
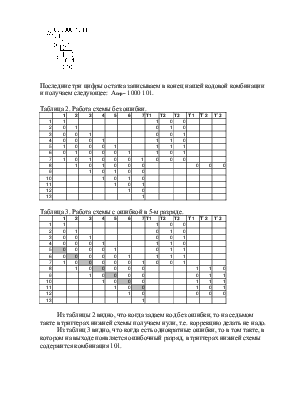
Последние три цифры остатка записываем в конец нашей
кодовой комбинации и получаем следующее: Апер=
1000 101.
Таблица 2. Работа схемы без ошибки.



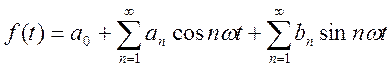 , где n=1,2,3…
, где n=1,2,3…![]() , где А – амплитуда
, где А – амплитуда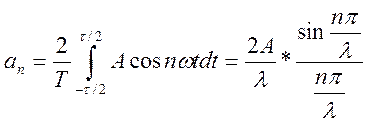 , где l - скважность.
, где l - скважность.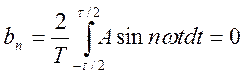
![]() ?
?