Информатика и выч. техника \ Кодирование и передача информации

Построение спектров периодических функций. Преобразование исходных функций к ряду Фурье. Знакомство с циклическим кодом, страница 2

	1	2	3	4	5	6	7	Т1	Т2	Т3	Т`1	T`2	Т`3
1	1							1	0	0
2	0	1						0	1	0
3	0	0	1					0	0	1
4	0	0	0	1				1	1	0
5	1	0	0	0	1			1	1	1
6	0	1	0	0	0	1		1	0	1
7	1	0	1	0	0	0	1	0	0	0
8		1	0	1	0	0	0				0	0	0
9			1	0	1	0	0
10				1	0	1	0
11					1	0	1
12						1	0
13							1

Таблица 3. Работа схемы с ошибкой в 5-м разряде.

	1	2	3	4	5	6	7	Т1	Т2	Т3	Т`1	T`2	Т`3
1	1							1	0	0
2	0	1						0	1	0
3	0	0	1					0	0	1
4	0	0	0	1				1	1	0
5	0	0	0	0	1			0	1	1
6	0	0	0	0	0	1		1	1	1
7	1	0	0	0	0	0	1	0	0	1
8		1	0	0	0	0	0				1	1	0
9			1	0	0	0	0				0	1	1
10				1	0	0	0				1	1	1
11					1	0	0				1	0	1
12						1	0				0	0	0
13							1

Из таблицы 2 видно, что когда задаем код без ошибки, то на седьмом такте в триггерах нижней схемы получаем нули, т.е. коррекцию делать не надо.

Из таблиц 3 видно, что когда есть однократные ошибки, то в том такте, в котором на выходе появляется ошибочный разряд, в триггерах нижней схемы содержится комбинация 101.

Исходя из этого определяем вид ЛС.

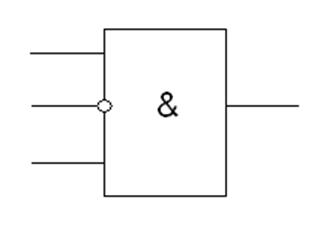
Сигнал Q нужен для того, чтобы обнулять триггеры нижней схемы. Такт 12, в таблице 3 с ошибкой в 5-м разряде, посчитан с учетом того, что на этом такте сигнал Q = 1.

Вывод.

В ходе проделанной работы мы научились строить спектры периодических функций, делать преобразования исходных функций к ряду Фурье, а также познакомились с циклическим кодом.

1 2

Скачать файл