

Тема 5. Вопрос 2.
Размах
варьирования![]() . Для определения размаха
необходимо расположить единицы выборки в возрастающем, или убывающем порядке.
. Для определения размаха
необходимо расположить единицы выборки в возрастающем, или убывающем порядке.
Среднее
значение выборки случайной величины, или выборочное среднее вычисляется по
формуле средней арифметической 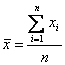 (4),
(4),
или для
упорядоченного ряда по формуле средней арифметической взвешенной  (5).
(5).
Если значения ![]() велики, то вычисления
можно упростить, введя условную
среднюю, которую обозначим через
велики, то вычисления
можно упростить, введя условную
среднюю, которую обозначим через ![]() . Тогда получим
. Тогда получим
![]() (6).
(6).
Медиана – значение, расположенное в середине упорядоченного ряда значений выборки. Если упорядоченный ряд дискретный и состоит из нечетного числа членов, то медианой будет среднее значение ряда; если число членов нечетное – среднее арифметическое двух соседних значений, находящихся в середине ряда.
Медиана
интервального ряда данных определяется по формуле 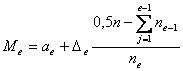 (7),
где
(7),
где
![]() - начальное значение интервала,
содержащего медиану;
- начальное значение интервала,
содержащего медиану;
![]() - величина интервала группировки;
- величина интервала группировки;
![]() - сумма накопленных частот для
интервалов, предшествующих медианному;
- сумма накопленных частот для
интервалов, предшествующих медианному;
(![]() )- номер интервала, предшествующего
медианному;
)- номер интервала, предшествующего
медианному;
![]() - частота медианного интервала.
- частота медианного интервала.
Дисперсия - статистическая характеристика ряда наблюдаемых значений показывающая как тесно группируются отдельные значения вокруг средней арифметической или как они рассеиваются вокруг этой средней.
Алгебраическая сумма
отклонений отдельных значений xi от средней арифметической ![]() равна
нулю. Поэтому она не пригодна в качестве меры рассеяния. Поэтому за меру рассеяния
принимают сумму квадратов отклонений от
равна
нулю. Поэтому она не пригодна в качестве меры рассеяния. Поэтому за меру рассеяния
принимают сумму квадратов отклонений от
дельных значений от средней
арифметической, деленную на количество наблюдений. Эту меру называют
дисперсией и обозначают через ![]()
![]() (8)
(8)
Вычисление дисперсии упорядоченного ряда пользуются следующей формулой
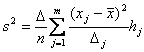 (9)
(9)
или, если введена условная средняя ![]()
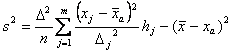 (10).
(10).
Среднее квадратическое
отклонение ![]() часто применяют вместо дисперсии
часто применяют вместо дисперсии ![]() . Оно имеет ту же размерность, что и средняя арифметическая
. Оно имеет ту же размерность, что и средняя арифметическая ![]() .
.
![]() (9)
(9)
Коэффициент
асимметрии вычисляется по формуле: ![]() ,
где
,
где ![]()
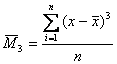 -
выборочный центральный момент 3-го порядка.
-
выборочный центральный момент 3-го порядка.
Выборочный
эксцесс определяется следующим образом: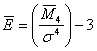 ,
где
,
где 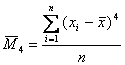 - выборочный центральный момент
4-го порядка.
- выборочный центральный момент
4-го порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.