Уравнение линейной регрессии

Тема 5. Вопрос 14

Уравнение линейной регрессии

В 1886 г. генетик Фрэнсис Гальтон (Ргапсез ОаИоп) за­метил, что родители большого роста имеют преимуществен­но и детей большого роста, а родители небольшого роста — детей небольшого роста.  Поскольку рост потомства стремится двигаться к сред­нему, Гальтон назвал это явление регрессией к среднему, а линию, проходящую через точки на графике,— линией ре­грессии. Термин «линия регрессии» употребляется теперь для линий наилучшей подгонки (в смысле, который поясня­ется ниже) под экспериментальные точки вне зависимости от того, имеется ли регрессия к среднему в смысле Гальтона.

Исследование чисто прямолинейных зависимостей, встре­чающихся в физике, например закона Гука или зависимости между током и напряженном для цепи с постоянным сопро­тивлением в соответствии с законом Ома, вряд ли является задачей статистики.

Пусть в качестве эмпирической формулы функции Y=F(X) взята линейная функция и задача сводится к отысканию таких значений парамет­ров и , при которых функция

принимает наименьшее значение. Функция есть функция двух переменных и до тех пор, пока не найдены их «наилучшие» (в смысле метода наименьших квадратов) значения. Следовательно, для нахождения прямой, наилучшим образом согласованной с  опытными данными достаточно решить систему, приравняв нулю частные производные  подбираемой линейной функции:

           ,или                         

                                 

После алгебраических преобразований эта система принимает вид:

Полученная система нормальных уравнений имеет единственное решение , соответствующее минимуму функции .

ПРИМЕР:

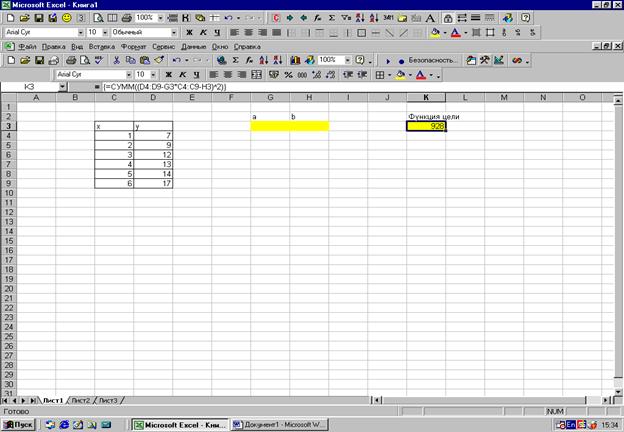
Вы менеджер недавно открывшегося салона по продаже автомобилей и постоянно ведете учет проданных автомобилей. В Вашем распоряжении имеются две наблюдаемые величины:

X – номер недели;

Y – число проданных за неделю автомобилей.

У Вас имеется статистика продаж за первые шесть недель.

Для решения этой задачи:

1.Заполните ячейки С4:С9 - значениями X, D4:D9 – значениями Y.

2.Отведите под переменные a, b ячейки G3, H3.

3.В ячейку K3 введите минимизируемую функцию. После нажатия ввода функции нажать комбинацию <Shift>+<Ctrl>+<Enter> (поскольку это функция массива).

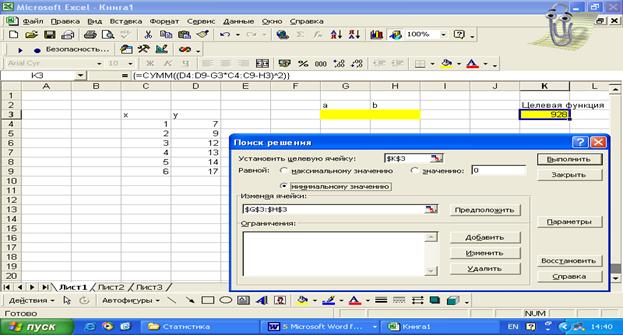
4.Выберите команду CЕРВИС-ПОИСК РЕШЕНИЯ.

Диалоговое окно ПОИСК РЕШЕНИЯ заполните, как показано на рисунке (на переменные a, b не налагаются никакие ограничения).

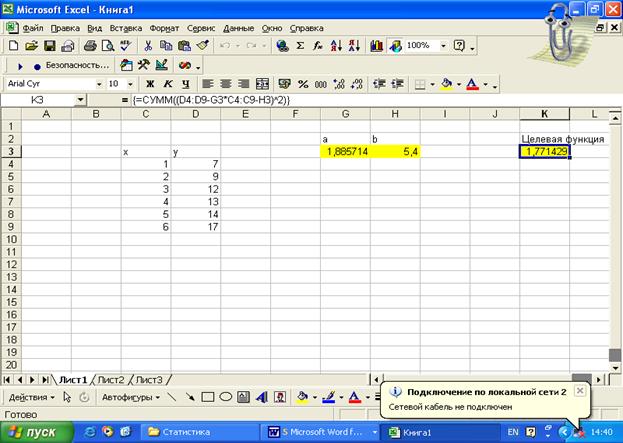
5.  Нажмите кнопку Выполнить. В результате вычислений ПОИСК РЕШЕНИЯ найдет a=1,88571 и b=5,400.