При создании единичной матрицы M1 используется функция if с условиями сравнения: если условие i=j (логическое равенство вводится комбинацией клавиш Ctrl + =) выполняется, то элементу матрицы присваивается значение 1, если условие не выполняется, то значение 0. Символ транспонирования матрицы может вводиться с помощью палитры Matrix: сначала в документе вводится имя матрицы, затем активизируется кнопка MTи вводится знак = для вывода результата. Ввод с клавиатуры символа транспонирования: Ctrl+!.
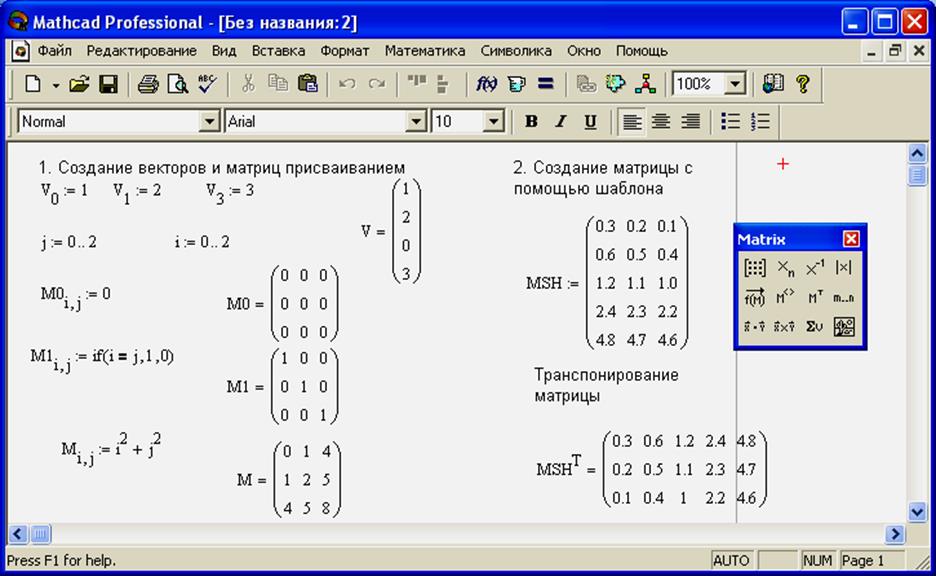
Рис.7. Способы задания матриц и векторов.
Задание. Измените условие заполнения матрицы М1 таким образом, чтобы матрица приняла вид:
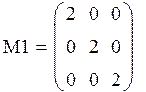
Вычислите обратную матрицу, используя палитру и используя клавиатуру.
Векторные и матричные операции и функции Mathcad позволяют решать широкий круг задач линейной алгебры. Если представить систему n линейных уравнений в матричной форме:
A*X=B, (1)
где A–матрица коэффициентов размером n* n, B– вектор свободных членов размерностью n, X – вектор решения, то решение можно получить в виде
X=A-1*B.
На рис.8 приведён пример решения системы линейных уравнений.
Поскольку решение систем линейных уравнений довольно распространённая задача, в Mathcad имеется встроенная функция
lsolve(A,B).
На рис.8 приведён пример применения этой функции.
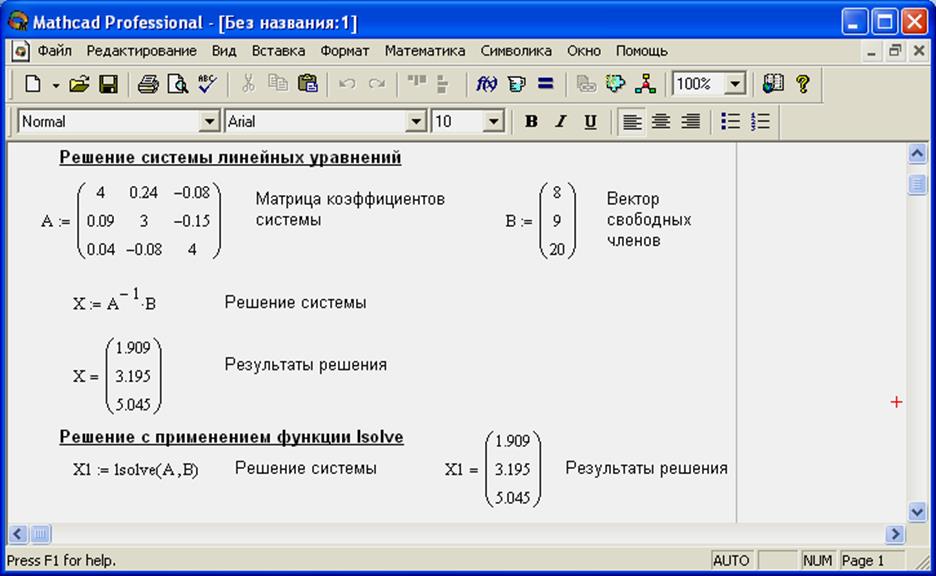
Рис.8. Решение систем линейных уравнений.
Задание для самостоятельной работы.
Найти решение системы линейных уравнений двумя рассмотренными выше способами. Выполнить проверку путём подстановки решения в матричное уравнение(1).
|
вариант |
Система линейных уравнений |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
2.7*Х1 + 3.3*Х2 + 1.3*Х3 =2.1 3.5*Х1 - 1.7*Х2 + 2.8*Х3 =1.7 4.1*Х1 + 5.8*Х2 - 1.7*Х3 =0.8 3.1*Х1 + 2.8*Х2 + 1.9*Х3 =0.2 1.9*Х1 + 3.1*Х2 + 2.1*Х3 =2.1 7.5*Х1 + 3.8*Х2 + 4.8*Х3 =5.6 1.7*Х1 + 2.8*Х2 + 1.9*Х3 =0.7 2.1*Х1 + 3.4*Х2 + 1.8*Х3 =1.1 4.2*Х1 - 1.7*Х2 + 1.3*Х3 =2.8 9.1*Х1 + 5.6*Х2 + 7.8*Х3 =9.8 3.8*Х1 + 5.1*Х2 + 2.8*Х3 =6.7 4.1*Х1 + 5.7*Х2 + 1.2*Х3 =5.8 3.3*Х1 + 2.1*Х2 + 2.8*Х3 =0.8 4.1*Х1 + 3.7*Х2 + 4.8*Х3 =5.7 2.7*Х1 + 1.8*Х2 + 1.1*Х3 =3.2 7.6*Х1 + 5.8*Х2 + 4.7*Х3 =10.1 3.8*Х1 + 4.1*Х2 + 2.7*Х3 =9.7 2.9*Х1 + 2.1*Х2 + 3.8*Х3 =7.8 3.2*Х1 - 2.5*Х2 + 3.7*Х3 =6.5 0.7*Х1 + 0.34*Х2 + 1.7*Х3 = -0.24 1.6*Х1 + 2.3*Х2 - 1.5*Х3 =4.3 5.4*Х1 - 2.3*Х2 + 3.4*Х3 = -3.5 4.2*Х1 + 1.7*Х2 - 2.3*Х3 =2.7 3.4*Х1 + 2.4*Х2 + 7.4*Х3 =1.9 3.6*Х1 + 1.8*Х2 – 4.7*Х3 =3.8 2.7*Х1 - 3.6*Х2 + 1.9*Х3 =0.4 1.5*Х1 + 4.5*Х2 + 3.3*Х3 = -1.6 5.6*Х1 + 2.7*Х2 - 1.7*Х3 =1.9 3.4*Х1 - 3.6*Х2 - 6.7*Х3 = -2.4 0.8*Х1 + 1.3*Х2 + 3.7*Х3 =1.2 2.7*Х1 + 0.9*Х2 - 1.5*Х3 =3.5 4.7*Х1 - 2.8*Х2 + 6.7*Х3 =2.6 5.1*Х1 + 3.7*Х2 - 1.4*Х3 = - 0.14 4.5*Х1 - 3.5*Х2 + 7.4*Х3 =2.5 3.1*Х1 - 0.6*Х2 - 2.3*Х3 = -1.5 0.8*Х1 + 7.4*Х2 - 0.5*Х3 =6.4 3.8*Х1 + 6.7*Х2 - 1.2*Х3 =5.2 6.4*Х1 + 1.3*Х2 - 2.7*Х3 =3.8 2.4*Х1 - 4.5*Х2 + 3.5*Х3 = -0.6 |
1. Назначение и особенности пакета Mathcad.
2. Перечислите основные элементы интерфейса пакета.
3. Назначение математической панели инструментов.
4. Палитры математических знаков.
5. Перечислите основные области документа Mathcad.
6. Как вставить текстовую область в документ Mathcad?
7. Чем отличается глобальное и локальное определение переменных? С помощью каких операторов определяются?
8. Какие системные (предопределенные) переменные Вам известны? Как узнать их значение?
9. Какие виды функций в Mathcad Вам известны?
10. Как вставить встроенную функцию в документ Mathcad?
11. С помощью каких операторов можно вычислить интегралы, суммы и произведения?
12. Как определить ранжированные переменные с произвольным шагом? Какой шаг по умолчанию?
13. Как определить индексированную переменную?
14. Какие виды массивов в Mathcad Вам известны?
15. Какая системная переменная определяет нижнюю границу индексации элементов массива?
16. Опишите способы создания массивов в Mathcad.
17. Охарактеризуйте способы решения систем линейных уравнений в Mathcad.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.