Оптимизация ХТП с использованием численных методов

Лабораторная работа №6  «Оптимизация ХТП с использованием численных методов»

Цель работы: Идентифицироватьс помощью ОЦКП математическое описание области поверхности отклика, близкой к экстремуму в виде квадратичной регрессии. Определить оптимальные условия проведения процесса в химическом реакторе:  значения факторов (температуры, времени и концентрации), при которых отклик (выход продукта) максимален, используя численные методы поиска экстремума функции отклика.

Постановка задачи.

Объектом оптимизации является химический реактор периодического действия, в котором выход продукта зависит от концентраций реагентов (C₁иC₂), температуры в реакторе (Т) и времени протекания реакции (τ)  (см. лаб. работы №3 и №4).  Для описания поверхности отклика, близкой к экстремуму необходимо определить область экспериментирования.  На основании результатов лаб. работы №4 необходимо выбрать центр плана и задать интервалы варьирования:

                        Δ Т = 10К,   Δ τ = 1мин,    ΔC₂ = 0.2моль/л.

В указанной области необходимо выполнить ортогональный центральный композиционный план и идентифицировать квадратичную регрессию. Рассматривая полученную регрессию как критерий оптимальности (целевую функцию), найти оптимальные значения факторов с помощью численного метода.

Решение задачи с помощью пакетов STATISTICAи MATHCAD

1. Составлениеплана.

          Планирование выполняется в модуле  Design & Analysis of Experiments (Statistics - Industrial Statistics & Six Sigma). В окне модуля выбирается тип плана Centralcomposite.., в закладке Design еxperiment, выбирается тип плана 3/1/16 (число факторов, число блоков, число опытов), ОК.

В закладке Displaydesign включить порядок опытов (Order of runs) стандартный и отображение факторов  Numbers(+1,-1). В закладке Designcharacteristicвыбрать расчёт альфа (звёздное плечо) для ортогонального плана – Compute alpha for orthogonality, щёлкнуть Summary.

  В появившейся таблице плана присвоить имена факторам (X1,X2,X3). В план следует добавить 3 столбца, в которых следует вычислить размерные факторы (T, TAU,C2) и столбец отклика (Y).

2. Ввод и обработка результатов эксперимента.

          В соответствии с размерным планом следует выполнить эксперимент с помощью программы RKTS и ввести значения отклика в столбец Y.  Далее необходимо выполнить анализ результатов планирования. Для этого в окне Design & AnalysisofCentralComposite… перейти на закладку  Analyzedesign, сделать назначения переменных: отклик, кодированные факторы, (блоковые переменные не указываются) и щёлкнуть ОК. Используя различные закладки в появившемся окне AnalysisofaCentralComposite…, следует выполнить полный анализ полученной модели:

·  Таблица с коэффициентами регрессии вызывается  на закладке ANOVA/Effectsщелчком по клавише Regressioncoefficients. По таблице следует определить факторы, оказывающие незначимое влияние на отклик,  записать уравнение регрессии, включающее только значимые факторы. Регрессия, включающая все рассчитанные коэффициенты при кодированных факторах, имеет вид:

Ŷ   =  b₀ + b₁ X₁ + b₂ X₂  +  b₃ X₃ + b₁₂X₁X₂ +  b₁₃X₁X₃ +  b₂₃X₂X₃ + b₁₁X²₁ +  b₂₂X²₂ + b₃₃X²₃                                                        (1)

·  Используя другие закладки, следует выполнить более подробный анализ данных на предмет проверки адекватности регрессии: на закладке Residual plots (графики остатков)  щёлкнуть клавишу Observed vs. predicted values (наблюдаемый и расчётный отклик); на закладке Review residuals (обзор остатков) щёлкнуть клавишу Display predicted … для вывода таблицы с наблюдаемым, расчётным откликом и остатками.

3. Поиск оптимального режима работы реактора.

Необходимо найти такие значения факторов X₁, X₂, X₃, при которых отклик      Ŷ, представленный в виде функции (1), примет максимальное значение. Достаточно просто задачи такого типа решаются в пакете MATHCAD.  Для этого надо создать документ, в котором реализуются следующие вычисления:

1.  задаётся максимизируемая функция, как функция пользователя, например

2.  задаются начальные приближения по оптимизируемым факторам, например

                                

             Следует в дальнейшем получить решение при различных начальных приближениях.

3.  задаются ограничения по оптимизируемым факторам (этот блок следует после ключевого слова , например

                        

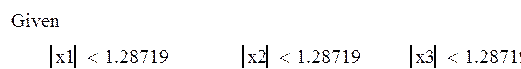
4.  выполняется поиск значений факторов, доставляющих экстремум функции f. Для этого можно использовать функцию maximize(f,x1,x2,x3), например

                           

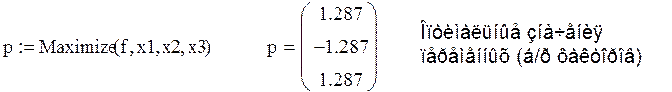
5.  рассчитывается максимальный отклик, соответствующий оптимальным значениям факторов, например

                                     

6.  определяются оптимальные значения размерных факторов по соответствующим формулам.

ПРИМЕЧАНИЕ:  Можно решать задачу оптимизации, используя целевую функцию не в кодированных, а в размерных факторах, тогда выполнять п.6 не требуется. Для этого следует  при обработке результатов эксперимента искать регрессию (1) в размерных факторах (T, TAU, C2), и при поиске оптимальных условий начальные приближения и ограничения по факторам задавать также в размерном виде.

Требования к оформлению лабораторной работы.

Отчет по лабораторной работе должен содержать:

·  название лабораторной работы;

·  цель работы;

·  ход решения задачи в STATISTICA с сопровождением полученных величин расчетными формулами и с подробным анализом полученных результатов;

·  документ MATHCADа с решением задачи оптимизации с различными начальными приближениями;

·  выводы по полученным результатам.