Описание промышленного контроллера FC-20 (Фирмы BECK), страница 2

                                                   

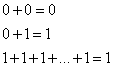
Операция логического умножения (конъюнкция) обознача­ется точкой или символом ^, или вообще в буквенных выраже­ниях никак не обозначается.

Функцию «И» реализуют, напри­мер, соединенные последовательно замыкающие контакты не­скольких реле. Цепь в этом случае будет замкнута только тогда, когда сработают все реле:

                                                           

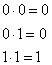
Логическое отрицание (инверсия) обозначается чертой или штрихом над обозначением аргумента. Моделью ячейки, реа­лизующей функцию НЕ, может служить размыкающий контакт реле. При срабатывании реле цепь, в которую входит такой кон­такт, будет размыкаться. Таким образом, инверсия единицы равна нулю, инверсия нуля — единице, а двойная инверсия не изменяет значения переменной.

                                                             

Основываясь на приведенных числовых равенствах, можно записать следующие выражения, в которых переменная, а может принимать значение 0 или 1:

                                                    

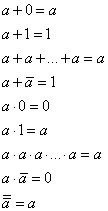
Основные законы алгебры логики.

Переместительный закон:

Сочетательный закон:

                                               

Распределительный закон:

                                                

Закон поглощения:

                                                

Закон склеивания:

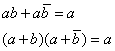
Закон   отрицания,   часто   называемый  также  правилом  де Моргана, справедлив для любого числа переменных:

                                           

Функционально полная система логических  элементов — это такой набор элементов, используя который, можно реализовать любую сколь угодно сложную логическую функцию. Поскольку любая логическая функция есть комбинация простейших функ­ций - дизъюнкции, конъюнкции и инверсии, то набор из эле­ментов трех типов, реализующих соответственно функции И, ИЛИ и НЕ, естественно, является функционально полным.

На­пример, функцию  можно реализовать с помощью двух ячеек НЕ (они нужны, чтобы получить инверсии  и ), двух ячеек И, необходимых для того, чтобы получить логические произведения  и , и ячейки ИЛИ, суммирующей эти произ­ведения.

Функционально полные системы могут состоять и из набора элементов, реализующих логические функции, отличные от про­стейших. В частности, функционально полные системы могут состоять из элементов только одного типа, например реализую­щих функцию И — НЕ либо ИЛИ — НЕ.

Функция И — НЕ, носящая также название функции Шеффера, означает следующее преобразование:

                                                        

Для того чтобы доказать функциональную полноту набора элементов, реализующих функцию И — НЕ, покажем возмож­ность построения на их основе логических цепей, реализующих простейшие функции.

Функцию НЕ, т. е. инвертирование пере­менной, можно реализовать, если сигнал, соответствующий этой переменной, подать на один из входов цепи И - НЕ, а на все остальные входы подать постоянный сигнал, соответствующий единице: . Для образования цепи И достаточно включить последовательно цепь И—НЕ и инвертор: . Цепь ИЛИ строится в соответствии с правилом де Моргана: . Таким образом, цепи И — НЕ позволяют реализовать инверсию, конъюнкцию и дизъюнкцию, а следовательно, на их основе можно строить логические цепи для реализации сколь угодно сложных функций.