Расчет неразрезной рамы

4.2. Расчет неразрезной рамы

4.2.1. Сбор нагрузок

I.  Постоянные нагрузки:

Нагрузки на стойки рамы от кровли:

На колонны:

Р_н= 0,55*4*4,5=10кН

Р_р=10*1,1=11кН

Нагрузки на ригели рамы от плит перекрытия:

На ригели верхних этажей:

Q_н= 8,32*4,5=37,44кН

Q_р=9,52*4,5=42,84кН

Нагрузки на пол подвала от конструкции пола подвала:

На пол подвала:

q_н= 0,2*24*4,5=19,64кН/м

q_р=19,64*1,1=21,6кН/м

II.  Временные нагрузки:

Нагрузки на стойки рамы от кровли:

На колонны:

Р_н= 1*6*4,5=22,9кН

Р_р=22,9*1,1=25,2кН

Нагрузки на ригели рамы от плит покрытия:

На ригели верхних этажей:

Q_н= 4*4,5=18кН

Q_р=4,8*4,5=21,6кН

Нагрузки на пол подвала от конструкции пола подвала:

На пол подвала:

q_н= 2*4,5=8,2кН/м

q_р=8,2*1,1=9кН/м

III.  Общие нагрузки

Нагрузки на стойки рамы от кровли:

На колонны:

Р_н= 15,3+10=25,3кН

Р_р=16,8+11=27,8кН

Нагрузки на ригели рамы от плит покрытия:

На ригели верхних этажей:

Q_н= 18+37,44=55,44кН

Q_р=21,6+42,84=64,44кН

Нагрузки на пол подвала от конструкции пола подвала:

На пол подвала:

q_н= 8,2+19,64=27,84кН/м

q_р=9+21,6=30,6кН/м

4.2.2. Определение усилий рамы

          Определение усилий рамы производим по программе «Strukcture CAD».

4.2.3. Расчет стойки

4.2.4 Подбор сечения арматуры

Для расчета принимаем два сечения с максимальной продольной силой и с максимальным изгибающим моментом.

 Сечение элемента размерами b = 400 мм, h = 400 мм; a = a' = 40 мм; бетон тя­желый класса В25 (E_b= 2,7 · 10⁴ МПа); арматура симметричная класса A-III (R_s =R_sc = 365 МПа; E_s = 2 · 10⁵ МПа); продольные силы и изгибающие моменты: от нагрузок N = 156,8 кН, M= 55,76 кН·м; расчетная длина l₀ = 3,6 м.

h₀ =400 – 40 = 360 мм.

Определим относительный эксцентриситет:

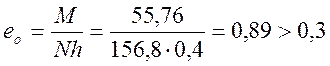
l₀/h = 360/40 = 9 < 10

значит сечение работает с большим эксцентриситетом

Определим момент силы N относительно оси растянутой арматуры по формуле:

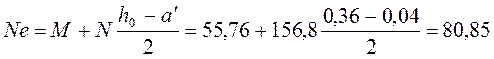 кН·м;

Определим площадь сечения сжатой арматуры по формуле:

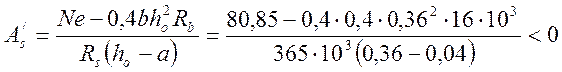
сжатую арматуру ставим из конструктивных соображений при минимальном проценте армирования . Принимаем 2 Ø 20 с А_s=6,28см².

Площадь растянутой арматуры определим по формуле:

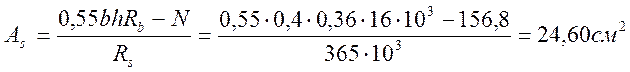
Принимаем 4 Ø 32 с А_s=24,63см².

Сечение элемента размерами b = 400 мм, h = 400 мм; a = a' = 40 мм; бетон тя­желый класса В25 (E_b= 2,7 · 10⁴ МПа); арматура симметричная класса A-III (R_s =R_sc = 365 МПа; E_s = 2 · 10⁵ МПа); продольные силы и изгибающие моменты: от нагрузок N = 1023,84 кН, M= 0,64 кН·м; расчетная длина l₀ = 0,5 м.

h₀ =400 – 40 = 360 мм.

Определим относительный эксцентриситет:

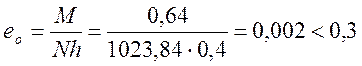
l₀/h = 50/40 = 1,25 < 10

значит сечение работает с большим эксцентриситетом

Определим момент силы N относительно оси растянутой арматуры по формуле:

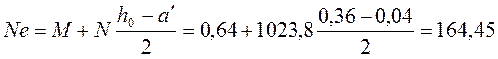 кН·м;

Определим площадь сечения сжатой арматуры по формуле:

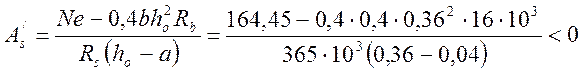
сжатую арматуру ставим из конструктивных соображений при минимальном проценте армирования . Принимаем 2 Ø 20 с А_s=6,28см².

Площадь растянутой арматуры определим по формуле:

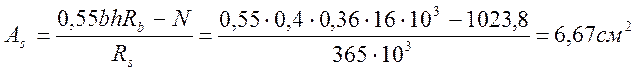
Принимаем 2 Ø 22 с А_s=7,6см².

4.2.5. Расчет сечени колонны на действие поперечных сил

Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине (черт. 13) производится из условия

                               (50)

где Q=28,42кН — поперечная сила от внешней нагрузки;

Q_b — поперечное усилие, воспринимаемое бе­тоном и равное:

             

  

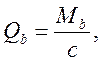
где j_b2=2 — коэффициент, учитывающий вид бетона и определяемый по табл. 21/1/;  

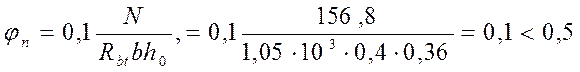
Диаметр поперечных стержней принимают из условия свариваемости с продольными стержнями ø16мм и принимаем ø4мм класса В-I, R_sw=290МПа (табл.23/1/) . число каркасов – два, А_sw=2*0,126=0,252см².

Шаг поперечных стержней по конструктивным  условиям s=h/2=30/2=15см, но не более 15см. в средине пролета s=(3/4)h=(3/4)40=30см, принимаем s=30см.

          Расчет ведем по формулам подглавы 3.3/3/.

Вычисляем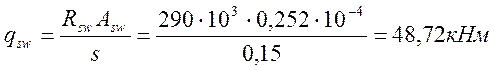

условие q_sw=48,72кН>Q_bmin/2=89,8/2=44,9кН удволетворяется.

          Требование 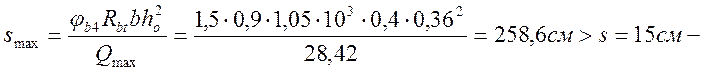условие удволетворяется.

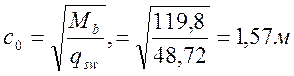принимаем с=157см.

         

тогда .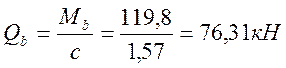

          Условие прочности Q_b+Q_sw=75,6+76,31=151,91кН>Q=28,42кН – обеспечино.

4.2.6. Расчет ригеля

4.2.7. Подбор сечения арматуры

          На отрицательный момент М=93,12кНм сечение работает как прямоугольное. Балка является не разрезной, следовательно максимальный момент возникает на опоре. Растягивающие усилия возникают в верхнем поясе.

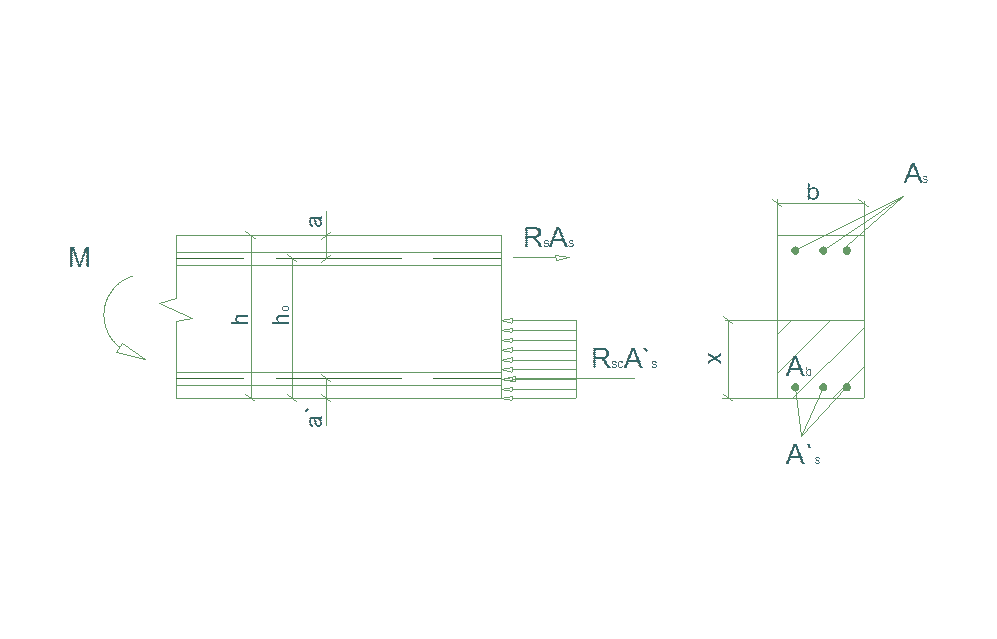
Рис. 4.8.Схема усилий в поперечном прямоугольном сече­нии

изгибаемого железобетонного элемента

h₀ =500 – 40 = 460 мм.

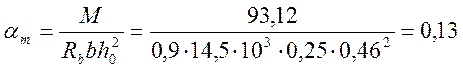(ф.22/6/)

по табл.20/6/  принимаем ζ=0,925.

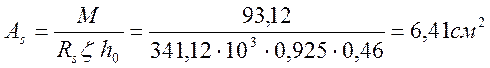
Принимаем два стержня 2ø22 А – III с А_s=7,6см².

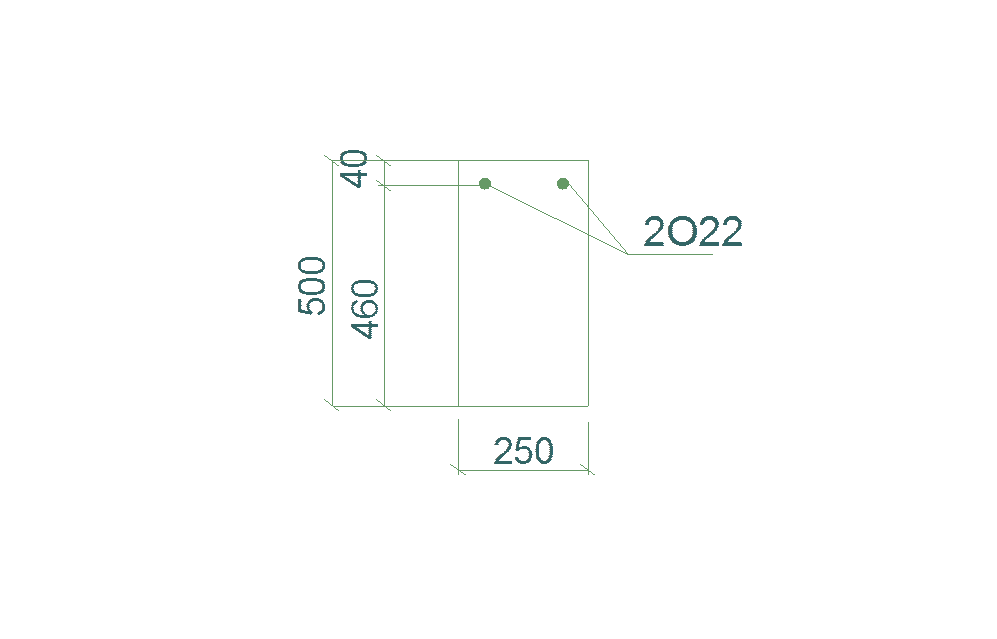
Рис. 4. 9. Схема армирования.

         

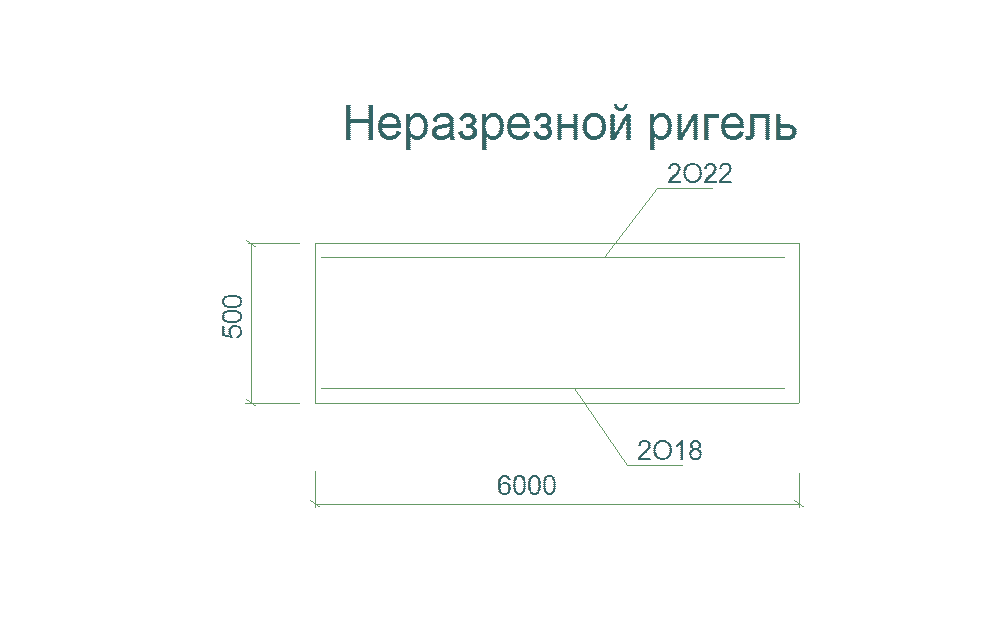
Рис. 4.11. Схема армирования балки.

4.2.8. Расчет прочности балки по сечениям,

Наклонным к продольной оси

          Диаметр поперечных стержней принимают из условия свариваемости с продольными стержнями ø22мм и принимаем ø4мм класса В-I, R_sw=290МПа (табл.23/1/) . число каркасов – два, А_sw=2*0,126=0,252см².

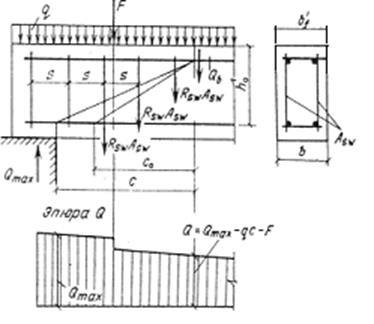
Рис.4.12. Схема усилий.

          Шаг поперечных стержней по конструктивным условиям s=h/2=50/2=25см, но не более 15см. для всех приопорных участков промежуточных и крайней опор балки принят шаг s=15см. в средине пролета s=(3/4)h=(3/4)50=37,5см, принимаем s=40см.

          Расчет ведем по формулам подглавы 3.3/3/.

Вычисляем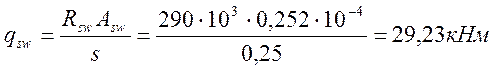

условие q_sw=29,23кН>Q_bmin/2=65,21/2=32,65кН удволетворяется.

          Требование 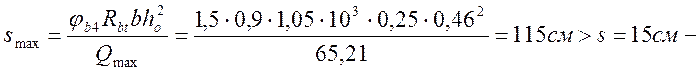условие удволетворяется.

При расчете прочности определим:

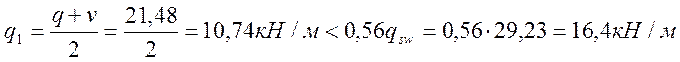
в связи сэтим следует вычислить:

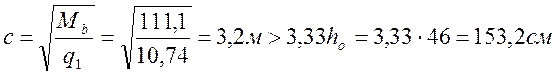
принимаем с=153,2см.

          тогда .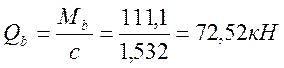

Длина проекции расчетного наклонного сечения:

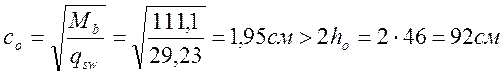
принимаем с=92см.

определим .

          Условие прочности Q_b+Q_sw=72,52+26,9=99,42кН>Q=69,08кН – обеспечино.

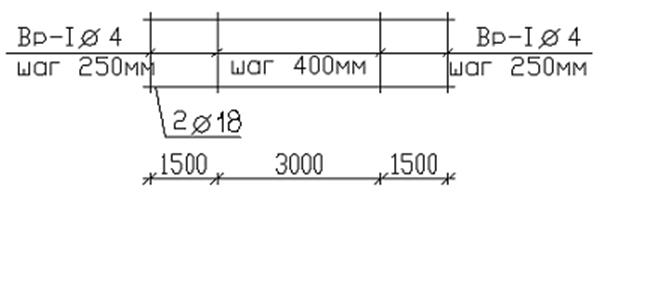
Рис. 4.13. Схема армирования.

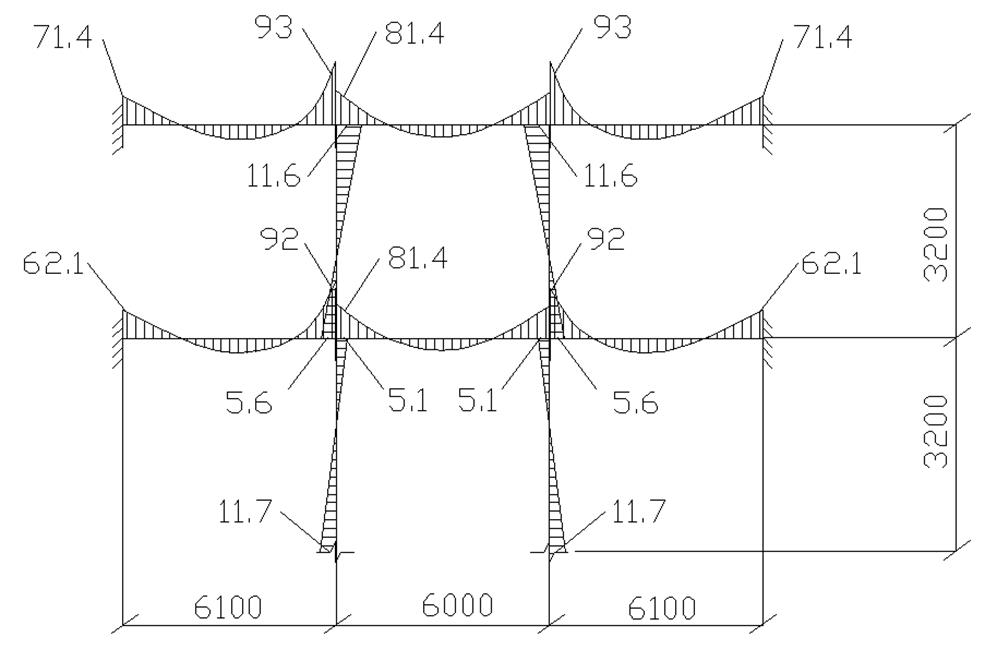
Рис. 4.14. Эпюра моментов рамы